title: 10. SVM(一)概念 date: 2018-07-02 16:27:00 categories: SVM tags: [SVM, 函数间隔, 几何间隔] mathjax: true
SVM,指的是支持向量机(support vector machines)。
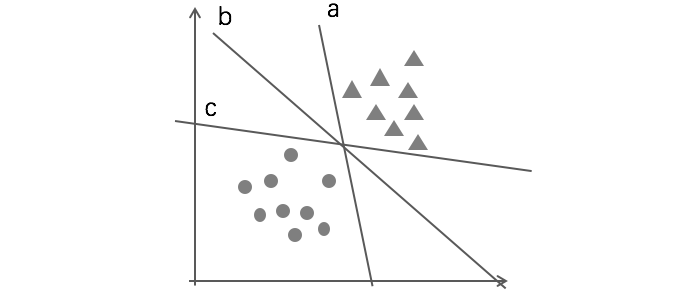
支持向量机,假设数据是线性可分的,那么我们就能找到一个超平面,将数据分成两类。但是一旦线性可分,我们就可能找到无数的超平面,都可以将数据分成两类:
但是很明显,上图中虽然a, c都对数据进行了有效的分割。但很明显,都不如b分割的好。
我们可以用“间隔”这个概念来定义这个超平面(在二维上是线)对数据的分割优劣。在分类正确的情况下,间隔越大,我们认为对数据的分类越好。
我们的目标是得到数据的分类:$y \in \lbrace -1, +1 \rbrace$。
这个超平面,则可以表示成$wTx+b$,其中$w=[\theta_1, \ldots, \theta_n]T, b=\theta_0$。这个超平面可以表达成一个$n+1$维向量。
判别函数: $$ g(z)=\begin{cases} +1, & \text{如果$z\geq0$} \
-1, & \text{otherwise} \end{cases} $$ 假设则可以表示成:$h_{w,b}(x)=g(w^Tx+b)$
间隔
函数间隔(functional margin)
某个超平面$(w,b)$和训练样本$(x{(i)}, y{(i)})$之间的函数间隔被表示成: $$ \hat{\gamma}{(i)}=y{(i)}(wTx{(i)}+b) $$ 于是,我们可以知道:
- 当$y{(i)}=1$,于是我们想获得更大的函数间隔(这是我们的目标),就需要使得$wTx^{(i)}+b \gg 0$
- 相反,当$y{(i)}=-1$,我们想获得更大的函数间隔,就需要使得$wTx^{(i)}+b \ll 0$
并且,很明显,只有当函数间隔$\hat{\gamma}>0$时,分类结果是正确的。
最后,超平面与数据集$\lbrace (x{(1)}, y{(1)}), (x{(2)}, y{(2)}), \ldots \rbrace$之间的函数间隔,被定义为所有函数间隔中的最小值: $$ \hat{\gamma}=\min_i\hat{\gamma}^{(i)} $$
几何间隔(geometric margin)
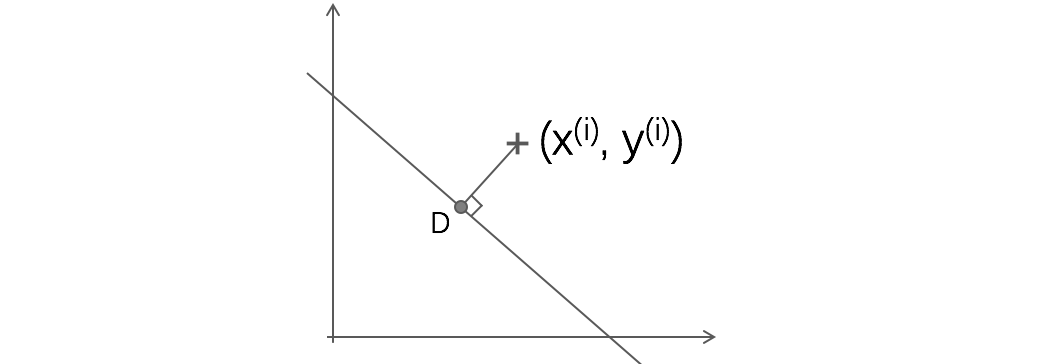
从点$(x{(i)}, y{(i)})$出发,对超平面做垂线,得到点D,我们知道他们之间的距离,就是该超平面到数据点$(x{(i)}, y{(i)})$的几何间隔。
经过推导,D的坐标可以表示为: $$ x{(i)}-\gamma{(i)}\frac{w}{||w||} $$ 又因为,D在超平面$wTx+b=0$上,所以: $$ \begin{align} & wT(x{(i)}-\gamma{(i)}\frac{w}{||w||})+b=0 \
& \Rightarrow wTx{(i)}+b=\gamma{(i)} \cdot \frac{wTw}{||w||}=\gamma{(i)} \cdot ||w|| \
& \Rightarrow \gamma{(i)}=(\frac{w}{||w||})T \cdot x{(i)}+\frac{b}{||w||} \end{align} $$ 加上正负分类的判断: $$ \gamma{(i)}=y{(i)} \cdot ((\frac{w}{||w||})T \cdot x{(i)}+\frac{b}{||w||}) $$ 我们可以看到,几何间隔跟函数间隔之间存在如下的关系: $$ \hat{\gamma}{(i)} = \frac{\gamma{(i)}}{||w||} $$
同样的,超平面与数据集$\lbrace (x{(1)}, y{(1)}), (x{(2)}, y{(2)}), \ldots \rbrace$之间的几何间隔,被定义为所有几何间隔中的最小值: $$ \gamma=\min_i\gamma{(i)} $$ 最后,我们导出最优间隔分类器(Optimal Margin Classifier)问题:选择$w, b$,最大化$\gamma$,同时满足$\forall(x{(i)}, y{(i)})$,$ y{(i)} \cdot ((\frac{w}{||w||})T \cdot x{(i)}+\frac{b}{||w||}) \geq \gamma$(所有数据点的几何间隔都大于该最小几何间隔)。
目前为止,已经是SVM问题的一个简化版本。