奇异值分解(SVD)原理与在降维中的应用

奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。本文就对SVD的原理做一个总结，并讨论在在PCA降维算法中是如何运用运用SVD的。

1. 回顾特征值和特征向量

我们首先回顾下特征值和特征向量的定义如下：$$Ax=\lambda x$$

其中A是一个$$n \times n$$的矩阵，x是一个n维向量，则我们说$$\lambda$$是矩阵A的一个特征值，而x是矩阵A的特征值$$\lambda$$所对应的特征向量。

求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵A特征分解。如果我们求出了矩阵A的n个特征值$$\lambda_1 \leq \lambda_2 \leq ... \leq \lambda_n$$,以及这n个特征值所对应的特征向量$${w_1,w_2,...w_n}$$，那么矩阵A就可以用下式的特征分解表示：$$A=W\Sigma W^{-1}$$

其中W是这n个特征向量所张成的$$n \times n$$维矩阵，而$$\Sigma$$为这n个特征值为主对角线的$$n \times n$$维矩阵。

一般我们会把W的这n个特征向量标准化，即满足$$||w_i||_2 =1$$, 或者说$$w_iTw_i =1$$，此时W的n个特征向量为标准正交基，满足$$WTW=I$$，即$$WT=W{-1}$$, 也就是说W为酉矩阵。

这样我们的特征分解表达式可以写成$$A=W\Sigma W^T$$

注意到要进行特征分解，矩阵A必须为方阵。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了。

2. SVD的定义

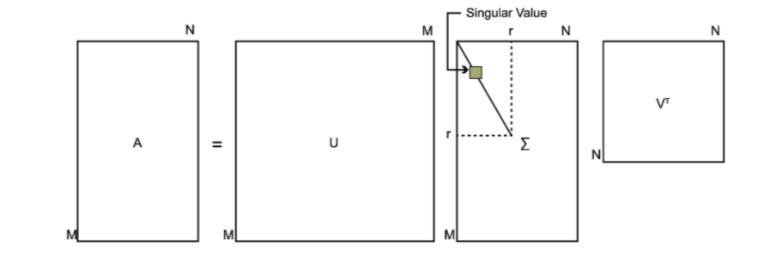
SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵A是一个$$m \times n$$的矩阵，那么我们定义矩阵A的SVD为：$$A = U\Sigma V^T$$

其中U是一个$$m \times m$$的矩阵，$$\Sigma$$是一个$$m \times n$$的矩阵，除了主对角线上的元素以外全为0，主对角线上的每个元素都称为奇异值，V是一个$$n \times n$$的矩阵。U和V都是酉矩阵，即满足$$UTU=I, VTV=I$$。下图可以很形象的看出上面SVD的定义：

那么我们如何求出SVD分解后的U, $$\Sigma$$, V这三个矩阵呢？

如果我们将A的转置和A做矩阵乘法，那么会得到$$n \times n$$的一个方阵$$ATA$$。既然$$ATA$$是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：$$(A^TA)v_i = \lambda_i v_i$$

这样我们就可以得到矩阵$$ATA$$的n个特征值和对应的n个特征向量v了。将$$ATA$$的所有特征向量张成一个$$n \times n$$的矩阵V，就是我们SVD公式里面的V矩阵了。一般我们将V中的每个特征向量叫做A的右奇异向量。

如果我们将A和A的转置做矩阵乘法，那么会得到$$m \times m$$的一个方阵$$AAT$$。既然$$AAT$$是方阵，那么我们就可以进行特征分解，得到的特征值和特征向量满足下式：$$(AA^T)u_i = \lambda_i u_i$$

这样我们就可以得到矩阵$$AAT$$的m个特征值和对应的m个特征向量u了。将$$AAT$$的所有特征向量张成一个$$m \times m$$的矩阵U，就是我们SVD公式里面的U矩阵了。一般我们将U中的每个特征向量叫做A的左奇异向量。

U和V我们都求出来了，现在就剩下奇异值矩阵$$\Sigma$$没有求出了。由于$$\Sigma$$除了对角线上是奇异值其他位置都是0，那我们只需要求出每个奇异值$$\sigma$$就可以了。

我们注意到:$$A=U\Sigma VT \Rightarrow AV=U\Sigma VTV \Rightarrow AV=U\Sigma \Rightarrow Av_i = \sigma_i u_i \Rightarrow \sigma_i = \frac {Av_i} {u_i}$$

这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵$$\Sigma$$。

上面还有一个问题没有讲，就是我们说$$ATA$$的特征向量组成的就是我们SVD中的V矩阵，而$$AAT$$的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。$$A=U\Sigma VT \Rightarrow AT=V\Sigma UT \Rightarrow ATA =V\Sigma UTU\Sigma VT = V\Sigma2VT$$

上式证明使用了:$$UTU=I, \SigmaT=\Sigma$$。可以看出$$ATA$$的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到$$AAT$$的特征向量组成的就是我们SVD中的U矩阵。

进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：$$\sigma_i = \sqrt{\lambda_i}$$

这样也就是说，我们可以不用$$\sigma_i =\frac {Av_i}{u_i}$$来计算奇异值，也可以通过求出$$A^TA$$的特征值取平方根来求奇异值。

3. SVD计算举例

这里我们用一个简单的例子来说明矩阵是如何进行奇异值分解的。我们的矩阵A定义为：

$$\mathbf{A} = \left( \begin{array}{ccc} 0& 1\ 1& 1\ 1&0 \end{array} \right)$$

我们首先求出$$ATA$$和$$AAT$$

$$\mathbf{A^TA} = \left( \begin{array}{ccc} 0& 1 &1\ 1&1&0 \end{array} \right) \left( \begin{array}{ccc} 0& 1\ 1& 1\ 1&0 \end{array} \right) = \left( \begin{array}{ccc} 2& 1 \ 1&2 \end{array} \right)$$

$$\mathbf{AA^T} = \left( \begin{array}{ccc} 0& 1\ 1& 1\ 1&0 \end{array} \right) \left( \begin{array}{ccc} 0& 1 &1\ 1&1&0 \end{array} \right) = \left(\begin{array}{ccc} 1& 1 &0\1& 2 &1\ 0& 1&1 \end{array} \right)$$

进而求出$$A^TA$$的特征值和特征向量：$$\lambda_1= 3; v_1 = \left( \begin{array}{ccc} \frac {1} {\sqrt{2}} \ \frac {1} {\sqrt{2}}\end{array} \right); \lambda_2= 1; v_2 = \left( \begin{array}{ccc} \frac {-1}{\sqrt{2}} \ \frac {1} {\sqrt{2}}\end{array} \right)$$

接着求$$AA^T$$的特征值和特征向量：

$$\lambda_1= 3; u_1 = \left( \begin{array}{ccc} \frac {1} {\sqrt{6}}\ \frac {2} {\sqrt{6}} \ \frac {1} {\sqrt{6}}\end{array} \right); \lambda_2= 1; u_2 = \left( \begin{array}{ccc} \frac {1} {\sqrt{2}} \ 0 \ \frac {-1} {\sqrt{2}}\end{array} \right); \lambda_3= 0; u_3 = \left( \begin{array}{ccc} \frac {1} {\sqrt{3}} \ \frac {-1} {\sqrt{3}}\ \frac {1} {\sqrt{3}}\end{array} \right)$$

利用$$Av_i = \sigma_i u_i, i=1,2$$求奇异值：

$$\left(\begin{array}{ccc} 0& 1\1& 1\ 1&0 \end{array} \right) \left( \begin{array}{ccc} \frac {1} {\sqrt{2}} \ \frac {1} {\sqrt{2}}\end{array} \right) = \sigma_1 \left( \begin{array}{ccc} \frac {1} {\sqrt{6}} \\frac {2} {\sqrt{6}} \ \frac {1} {\sqrt{6}}\end{array} \right)\Rightarrow \sigma_1=\sqrt{3}$$

$$\left( \begin{array}{ccc} 0& 1\1& 1\1&0 \end{array} \right) \left( \begin{array}{ccc} \frac {-1} {\sqrt{2}}\ \frac {1} {\sqrt{2}} \end{array} \right) = \sigma_2 \left( \begin{array}{ccc} \frac {1} {\sqrt{2}} \ 0 \ \frac {-1} {\sqrt{2}}\end{array} \right)\Rightarrow \sigma_2=1$$

当然，我们也可以用$$\sigma_i = \sqrt{\lambda_i}$$直接求出奇异值为$$\sqrt{3}$$和1.

最终得到A的奇异值分解为：$$A=U\Sigma V^T = \left( \begin{array}{ccc} \frac {1} {\sqrt{6}} & \frac {1} {\sqrt{2}} & \frac {1} {\sqrt{3}}\\frac {2} {\sqrt{6}} & 0 & \frac {-1} {\sqrt{3}}\ \frac {1} {\sqrt{6}} & \frac {-1} {\sqrt{2}} & \frac {1} {\sqrt{3}}\end{array} \right) \left( \begin{array}{ccc} \sqrt{3} & 0 \ 0 & 1\ 0 & 0 \end{array} \right) \left( \begin{array}{ccc} \frac {1} {\sqrt{2}}& \frac {1} {\sqrt{2}}\ \frac {-1} {\sqrt{2}}& \frac {1} {\sqrt{2}}\end{array} \right)$$

4. SVD的一些性质

上面几节我们对SVD的定义和计算做了详细的描述，似乎看不出我们费这么大的力气做SVD有什么好处。那么SVD有什么重要的性质值得我们注意呢？

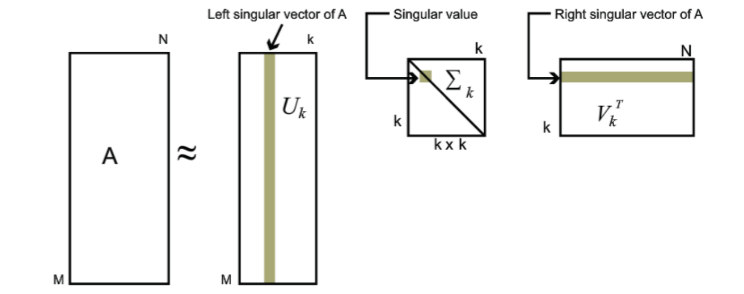
对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说：$$A_{m \times n} = U_{m \times m}\Sigma_{m \times n} VT_{n \times n} \approx U_{m \times k}\Sigma_{k \times k}VT_{k \times n}$$

其中k要比n小很多，也就是一个大的矩阵A可以用三个小的矩阵$$U_{m \times k},\Sigma_{k \times k} ,V^T_{k \times n}$$来表示。如下图所示，现在我们的矩阵A只需要灰色的部分的三个小矩阵就可以近似描述了。

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。下面我们就对SVD用于PCA降维做一个介绍。

5. SVD用于PCA

在主成分分析（PCA）原理总结中，我们讲到要用PCA降维，需要找到样本协方差矩阵$$XTX$$的最大的d个特征向量，然后用这最大的d个特征向量张成的矩阵来做低维投影降维。可以看出，在这个过程中需要先求出协方差矩阵$$XTX$$，当样本数多样本特征数也多的时候，这个计算量是很大的。

注意到我们的SVD也可以得到协方差矩阵$$XTX$$最大的d个特征向量张成的矩阵，但是SVD有个好处，有一些SVD的实现算法可以不求先求出协方差矩阵$$XTX$$，也能求出我们的右奇异矩阵V。也就是说，我们的PCA算法可以不用做特征分解，而是做SVD来完成。这个方法在样本量很大的时候很有效。实际上，scikit-learn的PCA算法的背后真正的实现就是用的SVD，而不是我们我们认为的暴力特征分解。

另一方面，注意到PCA仅仅使用了我们SVD的右奇异矩阵，没有使用左奇异矩阵，那么左奇异矩阵有什么用呢？

假设我们的样本是$$m \times n$$的矩阵X，如果我们通过SVD找到了矩阵$$XXT$$最大的d个特征向量张成的$$m\times d$$维矩阵U，则我们如果进行如下处理：$$X'{d\times n} = U{d \times m}TX_{m \times n}$$

可以得到一个$$d \times n$$的矩阵X‘,这个矩阵和我们原来的$$m\times n$$维样本矩阵X相比，行数从m减到了k，可见对行数进行了压缩。也就是说，左奇异矩阵可以用于行数的压缩。相对的，右奇异矩阵可以用于列数即特征维度的压缩，也就是我们的PCA降维。

6. SVD小结

SVD作为一个很基本的算法，在很多机器学习算法中都有它的身影，特别是在现在的大数据时代，由于SVD可以实现并行化，因此更是大展身手。SVD的原理不难，只要有基本的线性代数知识就可以理解，实现也很简单因此值得仔细的研究。当然，SVD的缺点是分解出的矩阵解释性往往不强，有点黑盒子的味道，不过这不影响它的使用。