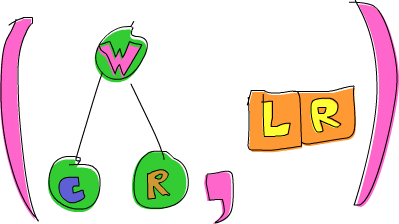Zippers 数据结构
尽管 Haskell 的纯粹性质带来很多好处,但他让一些在非纯粹语言很容易处理的一些事情变得要用另一种方法解决。由于 referential transparency,同样一件事在 Haskell 中是没有分别的。所以如果我们有一个装满 5 的树,而我们希望把其中一个换成 6,那我们必须要知道我们究竟是想改变哪个 5。我们也必须知道我们身处在这棵树的哪里。但在 Haskell 中,每个 5 都长得一样,我们并不能因为他们在内存中的地址不同就把他们区分开来。我们也不能改变任何状态,当我们想要改变一棵树的时候,我们实际上是说我们要一棵新的树,只是他长得很像旧的。一种解决方式是记住一条从根节点到现在这个节点的路径。我们可以这样表达:给定一棵树,先往左走,再往右走,再往左走,然后改变你走到的元素。虽然这是可行的,但这非常没有效率。如果我们想接连改变一个在附近的节点,我们必须再从根节点走一次。在这个章节中,我们会看到我们可以集中注意在某个数据结构上,这样让改变数据结构跟遍历的动作非常有效率。
来走二元树吧!
我们在生物课中学过,树有非常多种。所以我们来自己发明棵树吧!
data Tree a = Empty | Node a (Tree a) (Tree a) deriving (Show)
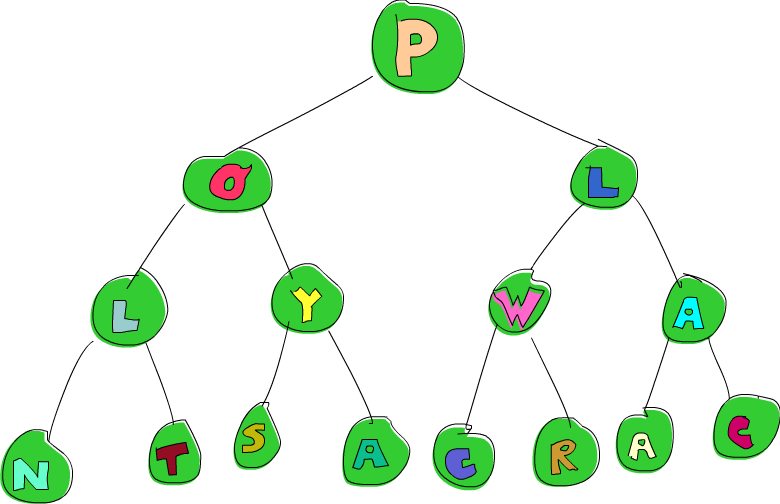
这边我们的树不是空的就是有两棵子树。来看看一个范例:
freeTree :: Tree Char
freeTree =
Node 'P'
(Node 'O'
(Node 'L'
(Node 'N' Empty Empty)
(Node 'T' Empty Empty)
)
(Node 'Y'
(Node 'S' Empty Empty)
(Node 'A' Empty Empty)
)
)
(Node 'L'
(Node 'W'
(Node 'C' Empty Empty)
(Node 'R' Empty Empty)
)
(Node 'A'
(Node 'A' Empty Empty)
(Node 'C' Empty Empty)
)
)
画成图的话就是像这样:
注意到 W 这个节点了吗?如果我们想要把他变成 P。我们会怎么做呢?一种方式是用 pattern match 的方式做,直到我们找到那个节点为止。要先往右走再往左走,再改变元素内容,像是这样:
changeToP :: Tree Char -> Tree Char
changeToP (Node x l (Node y (Node _ m n) r)) = Node x l (Node y (Node 'P' m n) r)
这不只看起来很丑,而且很不容易阅读。这到底是怎么回事?我们使用 pattern match 来拆开我们的树,我们把 root 绑定成 x,把左子树绑定成 l。对于右子树我们继续使用 pattern match。直到我们碰到一个子树他的 root 是 'W'。到此为止我们再重建整棵树,新的树只差在把 'W' 改成了 'P'。
有没有比较好的作法呢?有一种作法是我们写一个函数,他接受一个树跟一串 list,里面包含有行走整个树时的方向。方向可以是 L 或是 R,分别代表向左走或向右走。我们只要跟随指令就可以走达指定的位置:
data Direction = L | R deriving (Show)
type Directions = [Direction]
changeToP :: Directions-> Tree Char -> Tree Char
changeToP (L:ds) (Node x l r) = Node x (changeToP ds l) r
changeToP (R:ds) (Node x l r) = Node x l (changeToP ds r)
changeToP [] (Node _ l r) = Node 'P' l r
如果在 list 中的第一个元素是 L,我们会建构一个左子树变成 'P' 的新树。当我们递归地调用 changeToP,我们只会传给他剩下的部份,因为前面的部份已经看过了。对于 R 的 case 也一样。如果 list 已经消耗完了,那表示我们已经走到我们的目的地,所以我们就回传一个新的树,他的 root 被修改成 'P'。
要避免印出整棵树,我们要写一个函数告诉我们目的地究竟是什么元素。
elemAt :: Directions -> Tree a -> a
elemAt (L:ds) (Node _ l _) = elemAt ds l
elemAt (R:ds) (Node _ _ r) = elemAt ds r
elemAt [] (Node x _ _) = x
这函数跟 changeToP 很像,只是他不会记下沿路上的信息,他只会记住目的地是什么。我们把 'W' 变成 'P',然后用他来查看。
ghci> let newTree = changeToP [R,L] freeTree
ghci> elemAt [R,L] newTree
'P'
看起来运作正常。在这些函数里面,包含方向的 list 比较像是一种"focus",因为他特别指出了一棵子树。一个像 [R] 这样的 list 是聚焦在 root 的右子树。一个空的 list 代表的是主树本身。
这个技巧看起来酷炫,但却不太有效率,特别是在我们想要重复地改变内容的时候。假如我们有一个非常大的树以及非常长的一串包含方向的 list。我们需要沿着方向从 root 一直走到树的底部。如果我们想要改变一个邻近的元素,我们仍需要从 root 开始走到树的底部。这实在不太令人满意。
在下一个章节,我们会介绍一个比较好的方法,让我们可以有效率地改变我们的 focus。
凡走过必留下痕迹
我们需要一个比包含一串方向的 list 更好的聚焦的方法。如果我们能够在从 root 走到指定地点的沿路上撒下些面包屑,来纪录我们的足迹呢?当我们往左走,我们便记住我们选择了左边,当我们往右走,便记住我们选择了右边。
要找个东西来代表我们的面包屑,就用一串 Direction (他可以是 L 或者是 R),只是我们叫他 BreadCrumb 而不叫 Direction。这是因为现在我们把这串 direction 反过来看了:
type Breadcrumbs = [Direction]
这边有一个函数,他接受一棵树跟一些面包屑,并在我们往左走时在 list 的前头加上 L
goLeft :: (Tree a, Breadcrumbs) -> (Tree a, Breadcrumbs)
goLeft (Node _ l _, bs) = (l, L:bs)
我们忽略 root 跟右子树,直接回传左子树以及面包屑,只是在现有的面包屑前面加上 L。再来看看往右走的函数:
goRight :: (Tree a, Breadcrumbs) -> (Tree a, Breadcrumbs)
goRight (Node _ _ r, bs) = (r, R:bs)
几乎是一模一样。我们再来做一个先往右走再往左走的函数,让他来走我们的 freeTree
ghci> goLeft (goRight (freeTree, []))
(Node 'W' (Node 'C' Empty Empty) (Node 'R' Empty Empty),[L,R])
现在我们有了一棵树,他的 root 是 'W',而他的左子树的 root 是 'C',右子树的 root 是 'R'。而由于我们先往右走再往左走,所以面包屑是 [L,R]。
要再表示得更清楚些,我们能用定义一个 -:
x -: f = f x
他让我们可以将值喂给函数这件事反过来写,先写值,再来是 -:,最后是函数。所以我们可以写成 (freeTree, []) -: goRight 而不是 goRight (freeTree, [])。我们便可以把上面的例子改写地更清楚。
ghci> (freeTree, []) -: goRight -: goLeft
(Node 'W' (Node 'C' Empty Empty) (Node 'R' Empty Empty),[L,R])
Going back up
如果我们想要往回上走回我们原来的路径呢?根据留下的面包屑,我们知道现在的树是他父亲的左子树,而他的父亲是祖父的右子树。这些信息并不足够我们往回走。看起来要达到这件事情,我们除了单纯纪录方向之外,还必须把其他的数据都记录下来。在这个案例中,也就是他的父亲以及他的右子树。
一般来说,单单一个面包屑有足够的信息让我们重建父亲的节点。所以他应该要包含所有我们没有选择的路径的信息,并且他应该要纪录我们沿路走的方向。同时他不应该包含我们现在锁定的子树。因为那棵子树已经在 tuple 的第一个部份中,如果我们也把他纪录在面包屑里,那就会有重复的信息。
我们来修改一下我们面包屑的定义,让他包含我们之前丢掉的信息。我们定义一个新的型态,而不用 Direction:
data Crumb a = LeftCrumb a (Tree a) | RightCrumb a (Tree a) deriving (Show)
我们用 LeftCrumb 来包含我们没有走的右子树,而不仅仅只写个 L。我们用 RightCrumb 来包含我们没有走的左子树,而不仅仅只写个 R。
这些面包屑包含了所有重建树所需要的信息。他们像是软碟一样存了许多我们的足迹,而不仅仅只是方向而已。
大致上可以把每个面包屑想像成一个树的节点,树的节点有一个洞。当我们往树的更深层走,面包屑携带有我们所有走过得所有信息,只除了目前我们锁定的子树。他也必须纪录洞在哪里。在 LeftCrumb 的案例中,我们知道我们是向左走,所以我们缺少的便是左子树。
我们也要把 Breadcrumbs 的 type synonym 改掉:
type Breadcrumbs a = [Crumb a]
接着我们修改 goLeft 跟 goRight 来纪录一些我们没走过的路径的信息。不像我们之前选择忽略他。goLeft 像是这样:
goLeft :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goLeft (Node x l r, bs) = (l, LeftCrumb x r:bs)
你可以看到跟之前版本的 goLeft 很像,不只是将 L 推到 list 的最前端,我们还加入 LeftCrumb 来表示我们选择向左走。而且我们在 LeftCrumb 里面塞有我们之前走的节点,以及我们选择不走的右子树的信息。
要注意这个函数会假设我们锁定的子树并不是 Empty。一个空的树并没有任何子树,所以如果我们选择在一个空的树中向左走,就会因为我们对 Node 做模式匹配而产生错误。我们没有处理 Empty 的情况。
goRight 也是类似:
goRight :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goRight (Node x l r, bs) = (r, RightCrumb x l:bs)
在之前我们只能向左或向右走,现在我们由于纪录了关于父节点的信息以及我们选择不走的路的信息,而获得向上走的能力。来看看 goUp 函数:
goUp :: (Tree a, Breadcrumbs a) -> (Tree a, Breadcrumbs a)
goUp (t, LeftCrumb x r:bs) = (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = (Node x l t, bs)
我们锁定了 t 这棵树并检查最新的 Crumb。如果他是 LeftCrumb,那我们就建立一棵新的树,其中 t 是他的左子树并用关于我们没走过得右子树的信息来填写其他 Node 的信息。由于我们使用了面包屑的信息来建立父子树,所以新的 list 移除了我们的面包屑。
如果我们已经在树的顶端并使用这个函数的话,他会引发错误。等一会我们会用 Maybe 来表达可能失败的情况。
有了 Tree a 跟 Breadcrumbs a,我们就有足够的信息来重建整棵树,并且锁定其中一棵子树。这种方式让我们可以轻松的往上,往左,往右走。这样成对的数据结构我们叫做 Zipper,因为当我们改变锁定的时候,他表现得很像是拉链一样。所以我们便定义一个 type synonym:
type Zipper a = (Tree a, Breadcrumbs a)
我个人是比较倾向于命名成 Focus,这样可以清楚强调我们是锁定在其中一部分, 至于 Zipper 被更广泛地使用,所以这边仍维持叫他做 Zipper。
Manipulating trees under focus
现在我们具备了移动的能力,我们再来写一个改变元素的函数,他能改变我们目前锁定的子树的 root。
modify :: (a -> a) -> Zipper a -> Zipper a
modify f (Node x l r, bs) = (Node (f x) l r, bs)
modify f (Empty, bs) = (Empty, bs)
如果我们锁定一个节点,我们用 f 改变他的 root。如果我们锁定一棵空的树,那就什么也不做。我们可以移来移去并走到我们想要改变的节点,改变元素后并锁定在那个节点,之后我们可以很方便的移上移下。
ghci> let newFocus = modify (\_ -> 'P') (goRight (goLeft (freeTree,[])))
我们往左走,然后往右走并将 root 取代为 'P',用 -: 来表达的话就是:
ghci> let newFocus = (freeTree,[]) -: goLeft -: goRight -: modify (\_ -> 'P')
我们也能往上走并置换节点为 'X':
ghci> let newFocus2 = modify (\_ -> 'X') (goUp newFocus)
如果我们用 -: 表达的话:
ghci> let newFocus2 = newFocus -: goUp -: modify (\_ -> 'X')
往上走很简单,毕竟面包屑中含有我们没走过的路径的信息,只是里面的信息是相反的,这有点像是要把袜子反过来才能用一样。有了这些信息,我们就不用再从 root 开始走一遍,我们只要把反过来的树翻过来就好,然后锁定他。
每个节点有两棵子树,即使子树是空的也是视作有树。所以如果我们锁定的是一棵空的子树我们可以做的事就是把他变成非空的,也就是叶节点。
attach :: Tree a -> Zipper a -> Zipper a
attach t (_, bs) = (t, bs)
我们接受一棵树跟一个 zipper,回传一个新的 zipper,锁定的目标被换成了提供的树。我们不只可以用这招把空的树换成新的树,我们也能把现有的子树给换掉。让我们来用一棵树换掉我们 freeTree 的最左边:
ghci> let farLeft = (freeTree,[]) -: goLeft -: goLeft -: goLeft -: goLeft
ghci> let newFocus = farLeft -: attach (Node 'Z' Empty Empty)
newFocus 现在锁定在我们刚刚接上的树上,剩下部份的信息都放在面包屑里。如果我们用 goUp 走到树的最上层,就会得到跟原来 freeTree 很像的树,只差在最左边多了 'Z'。
I'm going straight to top, oh yeah, up where the air is fresh and clean!
写一个函数走到树的最顶端是很简单的:
topMost :: Zipper a -> Zipper a
topMost (t,[]) = (t,[])
topMost z = topMost (goUp z)
如果我们的面包屑都没了,就表示我们已经在树的 root,我们便回传目前的锁定目标。晡然,我们便往上走来锁定到父节点,然后递归地调用 topMost。我们现在可以在我们的树上四处移动,调用 modify 或 attach 进行我们要的修改。我们用 topMost 来锁定到 root,便可以满意地欣赏我们的成果。
来看串列
Zippers 几乎可以套用在任何数据结构上,所以听到他可以被套用在 list 上可别太惊讶。毕竟,list 就是树,只是节点只有一个儿子,当我们实作我们自己的 list 的时候,我们定义了下面的型态:
data List a = Empty | Cons a (List a) deriving (Show, Read, Eq, Ord)
跟我们二元树的定义比较,我们就可以看出我们把 list 看作树的原则是正确的。
一串 list 像是 [1,2,3] 可以被写作 1:2:3:[]。他由 list 的 head1 以及 list 的 tail 2:3:[] 组成。而 2:3:[] 又由 2 跟 3:[] 组成。至于 3:[],3 是 head 而 tail 是 []。
我们来帮 list 做个 zipper。list 改变锁定的方式分为往前跟往后(tree 分为往上,往左跟往右)。在树的情形中,锁定的部份是一棵子树跟留下的面包屑。那究竟对于一个 list 而言一个面包屑是什么?当我们处理二元树的时候,我们说面包屑必须代表 root 的父节点跟其他未走过的子树。他也必须记得我们是往左或往右走。所以必须要有除了锁定的子树以外的所有信息。
list 比 tree 要简单,所以我们不需要记住我们是往左或往右,因为我们只有一种方式可以往 list 的更深层走。我们也不需要哪些路径我们没有走过的信息。似乎我们所需要的信息只有前一个元素。如果我们的 list 是像 [3,4,5],而且我们知道前一个元素是 2,我们可以把 2 摆回 list 的 head,成为 [2,3,4,5]。
由于一个单一的面包屑只是一个元素,我们不需要把他摆进一个型态里面,就像我们在做 tree zippers 时一样摆进 Crumb:
type ListZipper a = ([a],[a])
第一个 list 代表现在锁定的 list,而第二个代表面包屑。让我们写一下往前跟往后走的函数:
goForward :: ListZipper a -> ListZipper a
goForward (x:xs, bs) = (xs, x:bs)
goBack :: ListZipper a -> ListZipper a
goBack (xs, b:bs) = (b:xs, bs)
当往前走的时候,我们锁定了 list 的 tail,而把 head 当作是面包屑。当我们往回走,我们把最近的面包屑欻来然后摆到 list 的最前头。
来看看两个函数如何运作:
ghci> let xs = [1,2,3,4]
ghci> goForward (xs,[])
([2,3,4],[1])
ghci> goForward ([2,3,4],[1])
([3,4],[2,1])
ghci> goForward ([3,4],[2,1])
([4],[3,2,1])
ghci> goBack ([4],[3,2,1])
([3,4],[2,1])
我们看到在这个案例中面包屑只不过是一部分反过来的 list。所有我们走过的元素都被丢进面包屑里面,所以要往回走很容易,只要把信息从面包屑里面捡回来就好。
这样的形式也比较容易看出我们为什么称呼他为 Zipper,因为他真的就像是拉链一般。
如果你正在写一个文本编辑器,那你可以用一个装满字串的 list 来表达每一行文本。你也可以加一个 Zipper 以便知道现在光标移动到那一行。有了 Zipper 你就很容易的可以添加或删除现有的每一行。
阳春的文件系统
理解了 Zipper 是如何运作之后,我们来用一棵树来表达一个简单的文件系统,然后用一个 Zipper 来增强他的功能。让我们可以在文件夹间移动,就像我们平常对文件系统的操作一般。
这边我们采用一个比较简化的版本,文件系统只有文件跟文件夹。文件是数据的基本单位,只是他有一个名字。而文件夹就是用来让这些文件比较有结构,并且能包含其他文件夹与文件。所以说文件系统中的组件不是一个文件就是一个文件夹,所以我们便用如下的方法定义型态:
type Name = String
type Data = String
data FSItem = File Name Data | Folder Name [FSItem] deriving (Show)
一个文件是由两个字串组成,代表他的名字跟他的内容。一个文件夹由一个字串跟一个 list 组成,字串代表名字,而 list 是装有的组件,如果 list 是空的,就代表他是一个空的文件夹。
这边是一个装有些文件与文件夹的文件夹:
myDisk :: FSItem
myDisk =
Folder "root"
[ File "goat_yelling_like_man.wmv" "baaaaaa"
, File "pope_time.avi" "god bless"
, Folder "pics"
[ File "ape_throwing_up.jpg" "bleargh"
, File "watermelon_smash.gif" "smash!!"
, File "skull_man(scary).bmp" "Yikes!"
]
, File "dijon_poupon.doc" "best mustard"
, Folder "programs"
[ File "fartwizard.exe" "10gotofart"
, File "owl_bandit.dmg" "mov eax, h00t"
, File "not_a_virus.exe" "really not a virus"
, Folder "source code"
[ File "best_hs_prog.hs" "main = print (fix error)"
, File "random.hs" "main = print 4"
]
]
]
这就是目前我的磁盘的内容。
A zipper for our file system
我们有了一个文件系统,我们需要一个 Zipper 来让我们可以四处走动,并且增加、修改或移除文件跟文件夹。就像二元树或 list,我们会用面包屑留下我们未走过路径的信息。正如我们说的,一个面包屑就像是一个节点,只是他包含所有除了我们现在正锁定的子树的信息。
在这个案例中,一个面包屑应该要像文件夹一样,只差在他缺少了我们目前锁定的文件夹的信息。为什么要像文件夹而不是文件呢?因为如果我们锁定了一个文件,我们就没办法往下走了,所以要留下信息说我们是从一个文件走过来的并没有道理。一个文件就像是一棵空的树一样。
如果我们锁定在文件夹 "root",然后锁定在文件 "dijon_poupon.doc",那面包屑里的信息会是什么样子呢?他应该要包含上一层文件夹的名字,以及在这个文件前及之后的所有项目。我们要的就是一个 Name 跟两串 list。借由两串 list 来表达之前跟之后的元素,我们就完全可以知道我们目前锁定在哪。
来看看我们面包屑的型态:
data FSCrumb = FSCrumb Name [FSItem] [FSItem] deriving (Show)
这是我们 Zipper 的 type synonym:
type FSZipper = (FSItem, [FSCrumb])
要往上走是很容易的事。我们只要拿现有的面包屑来组出现有的锁定跟面包屑:
fsUp :: FSZipper -> FSZipper
fsUp (item, FSCrumb name ls rs:bs) = (Folder name (ls ++ [item] ++ rs), bs)
由于我们的面包屑有上一层文件夹的名字,跟文件夹中之前跟之后的元素,要往上走不费吹灰之力。
至于要往更深层走呢?如果我们现在在 "root",而我们希望走到 "dijon_poupon.doc",那我们会在面包屑中留下 "root",在 "dijon_poupon.doc" 之前的元素,以及在他之后的元素。
这边有一个函数,给他一个名字,他会锁定在在现有文件夹中的一个文件:
import Data.List (break)
fsTo :: Name -> FSZipper -> FSZipper
fsTo name (Folder folderName items, bs) =
let (ls, item:rs) = break (nameIs name) items
in (item, FSCrumb folderName ls rs:bs)
nameIs :: Name -> FSItem -> Bool
nameIs name (Folder folderName _) = name == folderName
nameIs name (File fileName _) = name == fileName
fsTo 接受一个 Name 跟 FSZipper,回传一个新的 FSZipper 锁定在某个文件上。那个文件必须在现在身处的文件夹才行。这函数不会四处找寻这文件,他只会看现在的文件夹。
首先我们用 break 来把身处文件夹中的文件们分成在我们要找的文件前的,跟之后的。如果记性好,break 会接受一个 predicate 跟一个 list,并回传两个 list 组成的 pair。第一个 list 装有 predicate 会回传 False 的元素,而一旦碰到一个元素回传 True,他就把剩下的所有元素都放进第二个 list 中。我们用了一个辅助函数叫做 nameIs,他接受一个名字跟一个文件系统的元素,如果名字相符的话他就会回传 True。
现在 ls 一个包含我们要找的元素之前元素的 list。item 就是我们要找的元素,而 rs 是剩下的部份。有了这些,我们不过就是把 break 传回来的东西当作锁定的目标,来建造一个面包屑来包含所有必须的信息。
如果我们要找的元素不在文件夹中,那 item:rs 这个模式会符合到一个空的 list,便会造成错误。如果我们现在的锁定不是一个文件夹而是一个文件,我们也会造成一个错误而让程序当掉。
现在我们有能力在我们的文件系统中移上移下,我们就来尝试从 root 走到 "skull_man(scary).bmp" 这个文件吧:
ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsTo "skull_man(scary).bmp"
newFocus 现在是一个锁定在 "skull_man(scary).bmp" 的 Zipper。我们把 zipper 的第一个部份拿出来看看:
ghci> fst newFocus
File "skull_man(scary).bmp" "Yikes!"
我们接着往上移动并锁定在一个邻近的文件 "watermelon_smash.gif":
ghci> let newFocus2 = newFocus -: fsUp -: fsTo "watermelon_smash.gif"
ghci> fst newFocus2
File "watermelon_smash.gif" "smash!!"
Manipulating our file system
现在我们知道如何遍历我们的文件系统,因此操作也并不是难事。这边便来写个重命名目前锁定文件或文件夹的函数:
fsRename :: Name -> FSZipper -> FSZipper
fsRename newName (Folder name items, bs) = (Folder newName items, bs)
fsRename newName (File name dat, bs) = (File newName dat, bs)
我们可以重命名 "pics" 文件夹为 "cspi":
ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsRename "cspi" -: fsUp
我们走到 "pics" 这个文件夹,重命名他然后再往回走。
那写一个新的元素在我们目前的文件夹呢?
fsNewFile :: FSItem -> FSZipper -> FSZipper
fsNewFile item (Folder folderName items, bs) =
(Folder folderName (item:items), bs)
注意这个函数会没办法处理当我们在锁定在一个文件却要添加元素的情况。
现在要在 "pics" 文件夹中加一个文件然后走回 root:
ghci> let newFocus = (myDisk,[]) -: fsTo "pics" -: fsNewFile (File "heh.jpg" "lol") -: fsUp
当我们修改我们的文件系统,他不会真的修改原本的文件系统,而是回传一份新的文件系统。这样我们就可以访问我们旧有的系统(也就是 myDisk)跟新的系统(newFocus 的第一个部份)使用一个 Zippers,我们就能自动获得版本控制,代表我们能访问到旧的数据结构。这也不仅限于 Zippers,也是由于 Haskell 的数据结构有 immutable 的特性。但有了 Zipper,对于操作会变得更容易,我们可以自由地在数据结构中走动。
小心每一步
到目前为止,我们并没有特别留意我们在走动时是否会超出界线。不论数据结构是二元树,List 或文件系统。举例来说,我们的 goLeft 函数接受一个二元树的 Zipper 并锁定到他的左子树:
goLeft :: Zipper a -> Zipper a
goLeft (Node x l r, bs) = (l, LeftCrumb x r:bs)
但如果我们走的树其实是空的树呢?也就是说,如果他不是 Node 而是 Empty?再这情况,我们会因为模式匹配不到东西而造成 runtime error。我们没有处理空的树的情形,也就是没有子树的情形。到目前为止,我们并没有试着在左子树不存在的情形下锁定左子树。但要走到一棵空的树的左子树并不合理,只是到目前为止我们视而不见而已。
如果我们已经在树的 root 但仍旧试着往上走呢?这种情形也同样会造成错误。。用了 Zipper 让我们每一步都好像是我们的最后一步一样。也就是说每一步都有可能会失败。这让你想起什么吗?没错,就是 Monad。更正确的说是 Maybe monad,也就是有可能失败的 context。
我们用 Maybe monad 来加入可能失败的 context。我们要把原本接受 Zipper 的函数都改成 monadic 的版本。首先,我们来处理 goLeft 跟 goRight。函数的失败有可能反应在他们的结果,这个情况也不利外。所以来看下面的版本:
goLeft :: Zipper a -> Maybe (Zipper a)
goLeft (Node x l r, bs) = Just (l, LeftCrumb x r:bs)
goLeft (Empty, _) = Nothing
goRight :: Zipper a -> Maybe (Zipper a)
goRight (Node x l r, bs) = Just (r, RightCrumb x l:bs)
goRight (Empty, _) = Nothing
然后我们试着在一棵空的树往左走,我们会得到 Nothing:
ghci> goLeft (Empty, [])
Nothing
ghci> goLeft (Node 'A' Empty Empty, [])
Just (Empty,[LeftCrumb 'A' Empty])
看起来不错。之前的问题是我们在面包屑用完的情形下想往上走,那代表我们已经在树的 root。如果我们不注意的话那 goUp 函数就会丢出错误。
goUp :: Zipper a -> Zipper a
goUp (t, LeftCrumb x r:bs) = (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = (Node x l t, bs)
我们改一改让他可以失败得好看些:
goUp :: Zipper a -> Maybe (Zipper a)
goUp (t, LeftCrumb x r:bs) = Just (Node x t r, bs)
goUp (t, RightCrumb x l:bs) = Just (Node x l t, bs)
goUp (_, []) = Nothing
如果我们有面包屑,那我们就能成功锁定新的节点,如果没有,就造成一个失败。
之前这些函数是接受 Zipper 并回传 Zipper,这代表我们可以这样操作:
gchi> let newFocus = (freeTree,[]) -: goLeft -: goRight
但现在我们不回传 Zipper a 而回传 Maybe (Zipper a)。所以没办法像上面串起来。我们在之前章节也有类似的问题。他是每次走一步,而他的每一步都有可能失败。
幸运的是我们可以从之前的经验中学习,也就是使用 >>=,他接受一个有 context 的值(也就是 Maybe (Zipper a)),会把值喂进函数并保持其他 context 的。所以就像之前的例子,我们把 -: 换成 >>=。
ghci> let coolTree = Node 1 Empty (Node 3 Empty Empty)
ghci> return (coolTree,[]) >>= goRight
Just (Node 3 Empty Empty,[RightCrumb 1 Empty])
ghci> return (coolTree,[]) >>= goRight >>= goRight
Just (Empty,[RightCrumb 3 Empty,RightCrumb 1 Empty])
ghci> return (coolTree,[]) >>= goRight >>= goRight >>= goRight
Nothing
我们用 return 来把 Zipper 放到一个 Just 里面。然后用 >>= 来喂到 goRight 的函数中。首先我们做了一棵树他的左子树是空的,而右边是有两颗空子树的一个节点。当我们尝试往右走一步,便会得到成功的结果。往右走两步也还可以,只是会锁定在一棵空的子树上。但往右走三步就没办法了,因为我们不能在一棵空子树上往右走,这也是为什么结果会是 Nothing。
现在我们具备了安全网,能够在出错的时候通知我们。
我们的文件系统仍有许多情况会造成错误,例如试着锁定一个文件,或是不存在的文件夹。剩下的就留作习题。