感知机算法python实现
1.python代码实现
包含算法的原始形式和对偶形式
# -*- coding: utf-8 -*-
import numpy as np
class Perceptron(object):
def __init__(self, input_x, feature_num, input_y, learn_rate=1):
self._input_x = np.array(input_x) # 输入数据集中的X
self._input_y = np.array(input_y) # 输入数据集中的Y
self._feature_num = feature_num # 总共有多少个特征
self._rate = learn_rate # 学习速率
self._final_w = 0 # 最后学习到的w
self._final_b = 0 # 最后学习到的b
def sgd_train(self): #算法原始形式
total = len(self._input_y)
feature_num = range(self._feature_num)
data_num = range(total)
w = np.zeros(self._feature_num) #初始化向量w
b = 0
while True:
separted = True
for i in data_num: # 遍历数据集,查找误分类点
inner = np.inner(w, self._input_x[i])
if self._input_y[i] * (inner+b) <= 0: # 误分类点
separted = False
w = w + self._rate * self._input_y[i] * self._input_x[i]
b = b + self._rate * self._input_y[i]
if separted:
break
else:
continue
self._final_w = w
self._final_b = b
print(self._final_w, self._final_b)
def pair_sgd_train(self): # 对偶形式
total = len(self._input_y)
feature_num = range(self._feature_num)
data_num = range(total)
gram_matrix = self._input_x.dot(self._input_x.T) # Gram 矩阵
alpha = np.random.random(size=total) # 这里初始化alpha向量为随机值
b = 0
while True:
separted = True
for i in data_num:
inner = np.sum(alpha * self._input_y * gram_matrix[i])
if self._input_y[i] * (inner+b) <= 0: # 误分类点
separted = False
alpha[i] = alpha[i] + self._rate # 对偶形式只更新alpha向量中的一个分量
b = b + self._rate * self._input_y[i]
if separted:
break
else:
continue
self._final_w = (alpha * self._input_y.T).dot(self._input_x)
self._final_b = b
print(self._final_w, self._final_b)
input_x = [[3,3], [4,3], [1,1], [2,3]]
input_y = [1,1,-1,-1]
pla = Perceptron(input_x, 2, input_y, 1)
pla.sgd_train()
pla.pair_sgd_train()
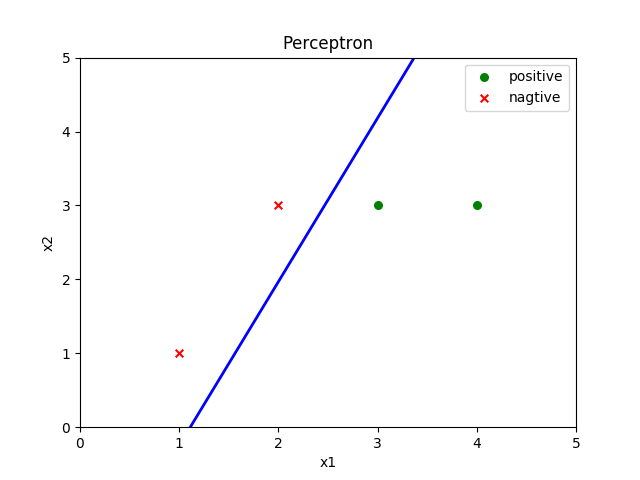
2. 图形显示
用matplotlib将结果用图形画出来,在类中添加如下函数
def draw_result(self):
total = len(self._input_y)
self._positive_x = []
self._nagtive_x = []
for i in range(total):
if self._input_y[i] >= 0:
self._positive_x.append(self._input_x[i])
else:
self._nagtive_x.append(self._input_x[i])
plt.figure(1)
x1 = [x[0] for x in self._positive_x]
x2 = [x[1] for x in self._positive_x]
plt.scatter(x1, x2, label='positive', color='g', s=30, marker="o") # 正数据集
x1 = [x[0] for x in self._nagtive_x]
x2 = [x[1] for x in self._nagtive_x]
plt.scatter(x1, x2, label='nagtive', color='r', s=30, marker="x") # 负数据集
plt.xlabel('x1')
plt.ylabel('x2')
plt.axis([0, 5, 0, 5])
def f(x):
return -(self._final_b + self._final_w[0]*x)/self._final_w[1]
x = np.array([0,1,2,3,4,5])
plt.plot(x, f(x), 'b-', lw=2) # 将最后的直线画出
plt.title('Perceptron')
plt.legend()
plt.show()
pla = Perceptron(input_x, 2, input_y, 1)
pla.pair_sgd_train()
pla.draw_result()
测试
input_x = [[3,3], [4,3], [1,1], [2,3]]
input_y = [1,1,-1,-1]
pla = Perceptron(input_x, 2, input_y, 1) # 2个特征,学习速率为1
pla.pair_sgd_train()
pla.draw_result()
参考文献:
http://blog.csdn.net/wangxin1982314/article/details/73529499
书籍推荐