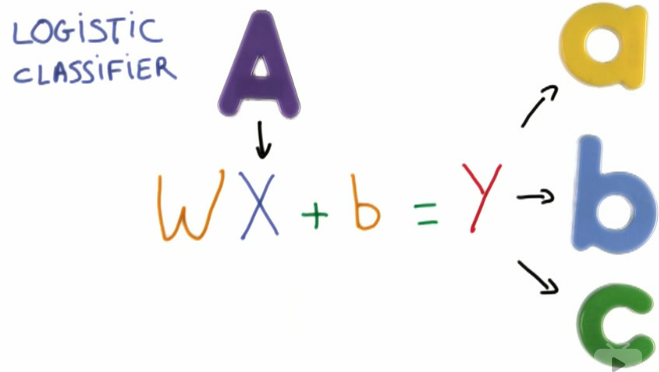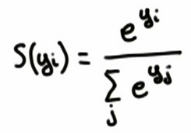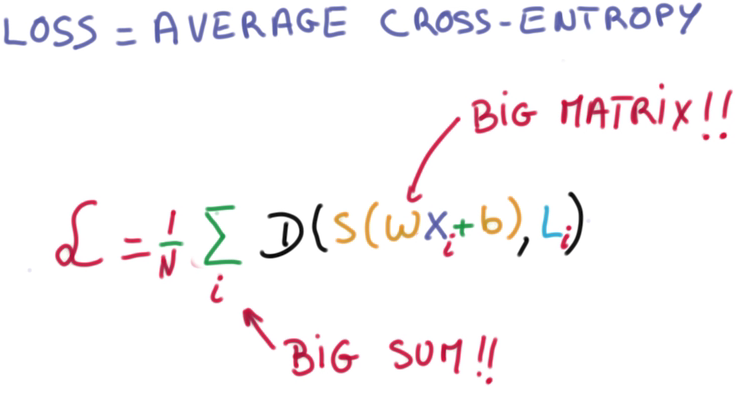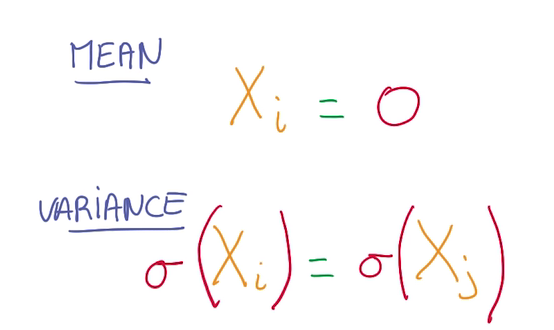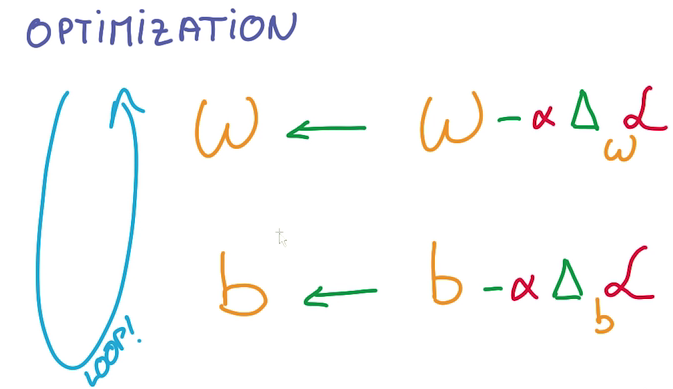Machine Lea..
Logistic Cl..

Google 深度学习笔记 (Google Deep Learning Notes)

Logistic Classification

Github工程地址：https://github.com/ahangchen/GDLnotes

欢迎star，有问题可以到Issue区讨论

官方教程地址

视频/字幕下载

About

simple but important classifier

  • 训练你的第一个端到端模型
  • 下载并预处理图片
  • 在图像数据上运行Logistic classifier进行分类
  • 相关的数学背景知识和代码

Detail

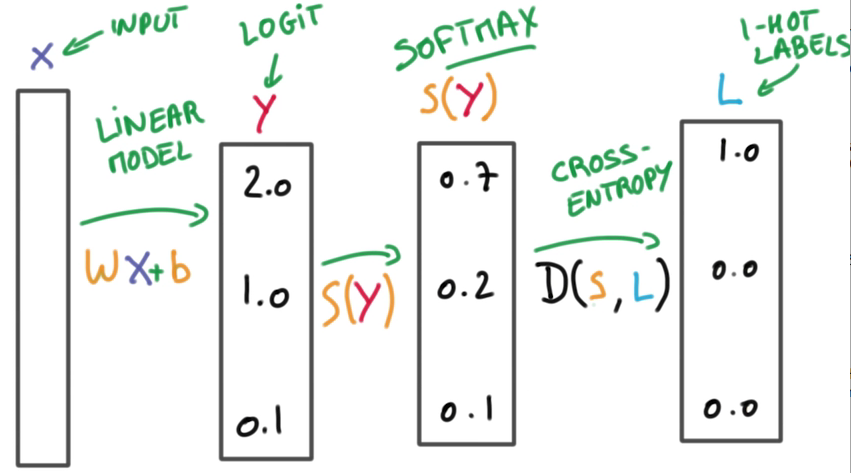
Linear Classifier

之所以这样建模，是因为线性公式是最简单的数学模型，仅此而已。

  • Input: X (e.g. 图像中像素的灰度值)

  • 将一个线性函数作用在X上  - 大矩阵相乘  - 输入一个代表图片的向量  - 将输入向量和一个矩阵W相乘，W表示权重  - b代表偏移（biased）项  - 机器学习便是调整权重和偏移值以达到最好的预测效果

  • 输出: Y, 对输入应当属于哪个类进行预测  - Y是一个代表每个label可能性的向量

    • 好的预测中，正确的label的概率应当更接近1
    • 往往得到的Y一开始不是概率，而是一些具体值（scores/logits），所以需要转换，by：

    Softmax回归模型：Wikipedia

Softmax

  • 代码 soft_max.py：Softmax实现与应用
  • input的score差异越大（可以全部乘10试试），则输出的各项label概率差异越大，反之差异越小
  • Softmax只关心几个label之间的概率，不关心具体值
  • 机器学习是一个让预测成功率升高的事情，因此是一个让score之间差异增大的过程

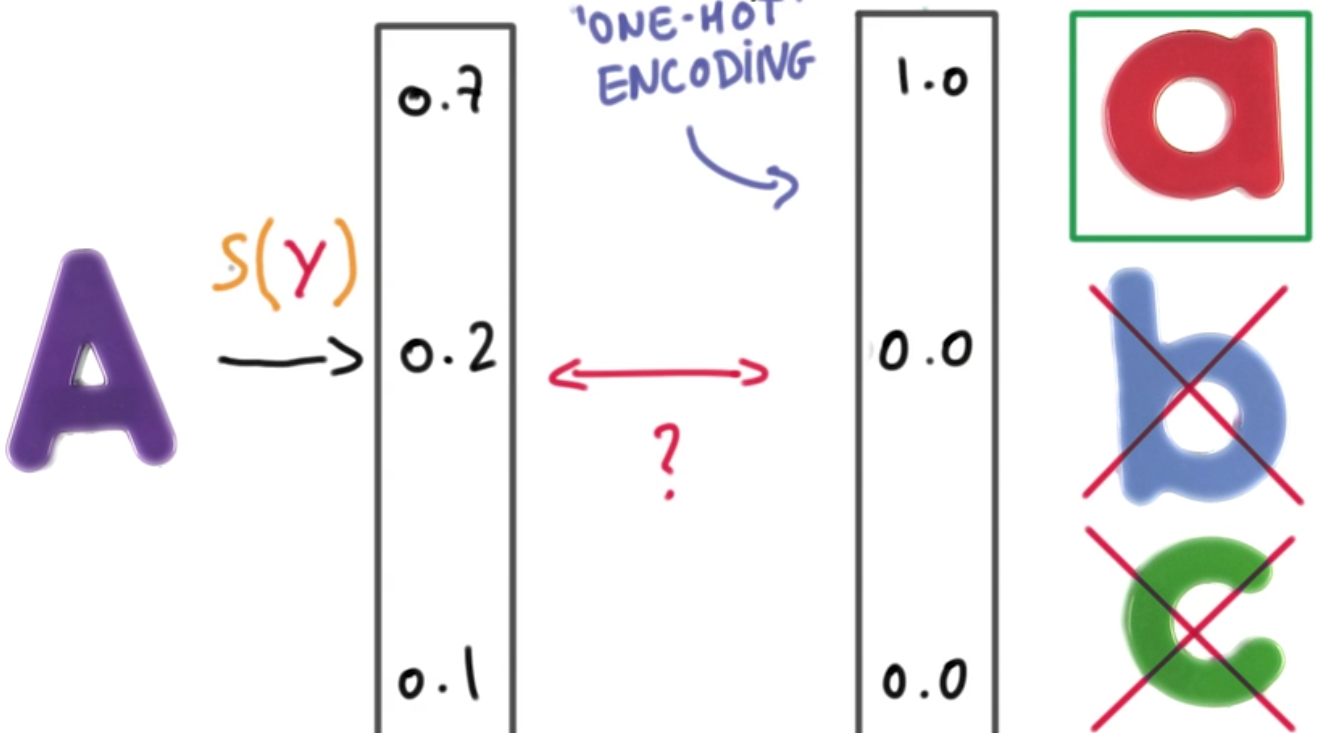
One hot encoding

正确预测结果应当是只有一个label成立，其他label不成立。这种情况下，预测概率最大的则是最可能的结果。

Example: take this test

 - one hot encoding在label很多的情况下效果不好，因为output vector到处都是0，很稀疏，因此效率低 - solved by embeddings

  • 好处：可以measure我们与理想情况之间的距离（compare two vectors）

分类器输出：[0.7 0.2 0.1] <=> 与label对应的真实情况：[1 0 0]

  • Compare two vectors: cross-entropy

  • D(S, L) != D(L, S)

Remember: Label don't log, for label zero

小结

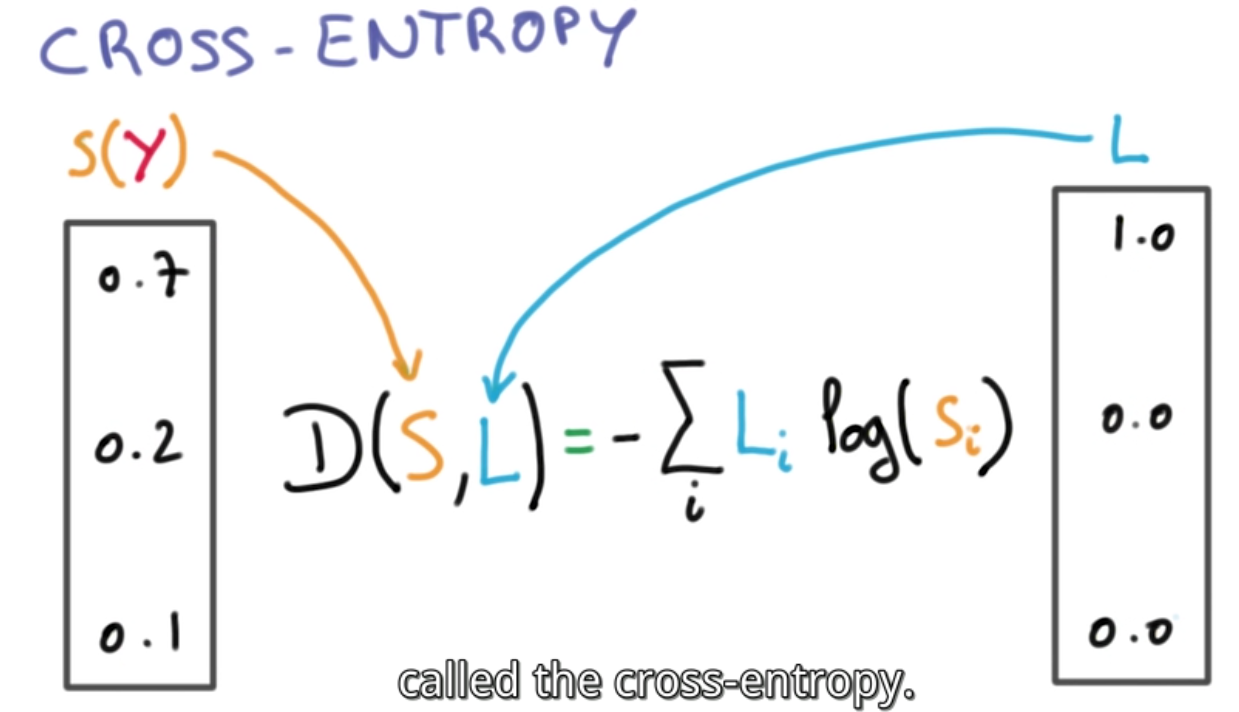
找到合适的W和b，使得S和L的距离D的平均值，在整个数据集n中最小。

最小化cross-entropy

D的平均值即是Training loss，求和和矩阵相乘是个大数据的活。

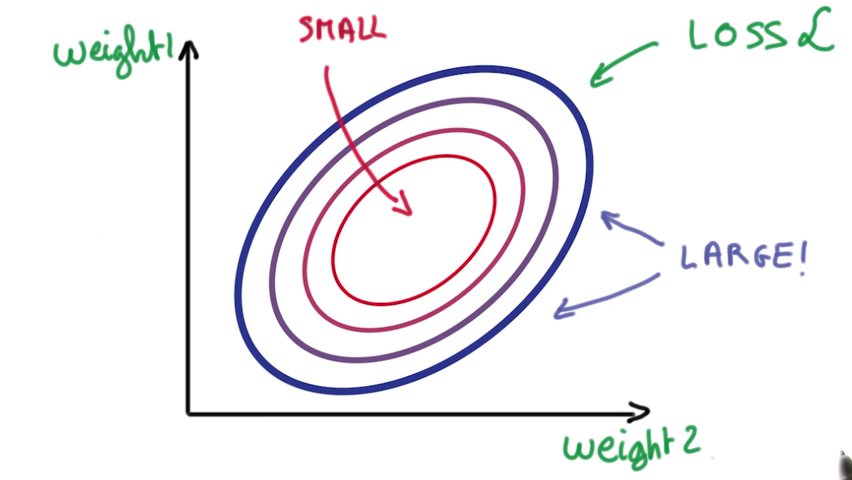
两个参数的误差导致一个呈圆形的loss，所以我们要做的就是找到尽量靠近圆心的weight

机器学习问题变成了一个数值优化

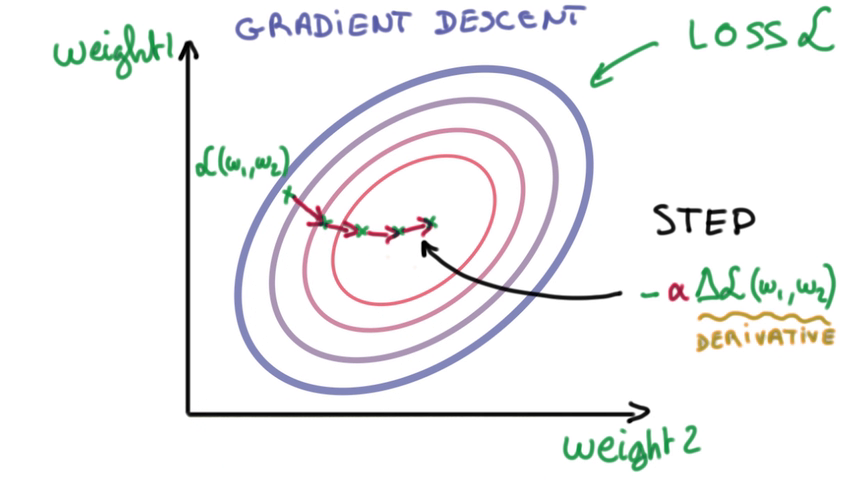
  • 解决方法之一：Gradient descent，求导

修改参数，检查误差是否变大，往变小的方向修改，直到抵达bottom。

图中weight是二维的，但事实上可能有极多的weight

Numerical Stability

量级相差太多的数运算会导致许多错误

Example:num_stable.py

  • 你可能以为输出是1， 但结果是一个接近0.95的数。
  • 但将1billion换成1，结果就很接近1。
  • 因此需要让前面提到的Train loss函数中的数据不要too big or too small

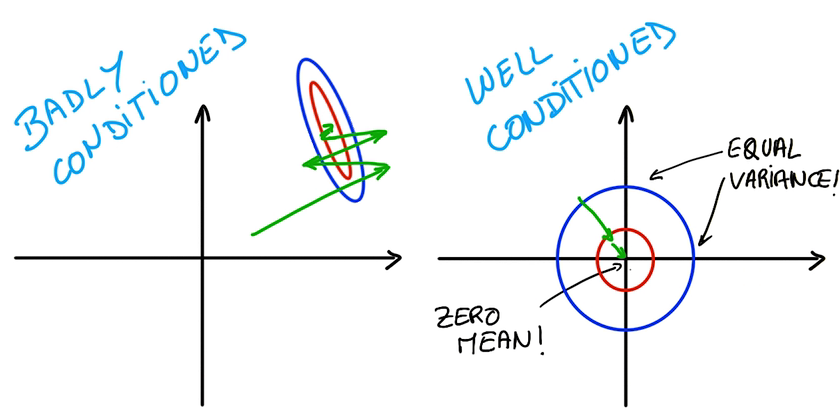
Normalized Inputs and Initial Wights

归一化输入和初始参数

  • 理想目标
    • 均值为0
    • 方差处处相等
  • Math Reason

Easier for the optimizer to find a good solution

  • Example: Images Normalization
R = (R - 128) / 128
G = (G - 128) / 128
B = (B - 128) / 128
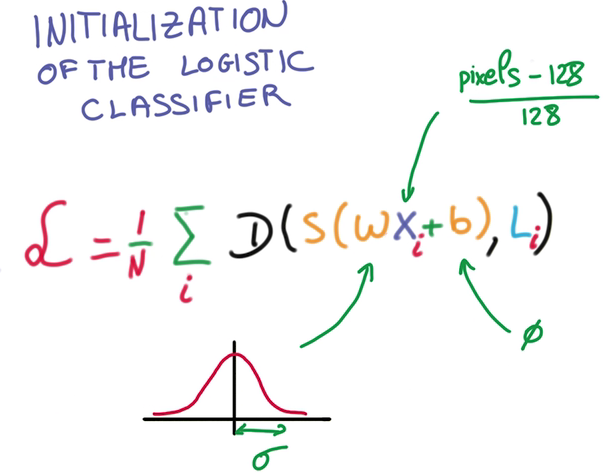
  • Weight Initialization 找到好的weight和bias for the gradient descent to proceed

A simple, general method

  • 用均值为0，标准偏差的高斯分布产生随机的数据填充W矩阵

  • 高斯分布模型也决定了初始输出(softmax输出)的概率分布

  • 高斯分布的sigma越小，说明预测越不确定，sigma的取值很主观

  • 我们的工作即是，选一个较小的sigma，让sigma变小到合适的值，使得预测更确定。

  • 优化 调整W和b，使得Train loss最小

扩展阅读：西瓜书第三章·线性模型 下一节实践

觉得得我的文章对您有帮助的话，就给个star吧～

书籍推荐