HMM前向后向算法评估观察序列概率

1. 回顾HMM问题一：求观测序列的概率

首先我们回顾下HMM模型的问题一。这个问题是这样的。我们已知HMM模型的参数$$\lambda = (A, B, \Pi)$$。其中A是隐藏状态转移概率的矩阵，B是观测状态生成概率的矩阵，$$\Pi$$是隐藏状态的初始概率分布。同时我们也已经得到了观测序列$$O ={o_1,o_2,...o_T}$$,现在我们要求观测序列O在模型$$\lambda$$下出现的条件概率$$P(O|\lambda)$$。

乍一看，这个问题很简单。因为我们知道所有的隐藏状态之间的转移概率和所有从隐藏状态到观测状态生成概率，那么我们是可以暴力求解的。

我们可以列举出所有可能出现的长度为T的隐藏序列$$I = {i_1,i_2,...,i_T}$$,分布求出这些隐藏序列与观测序列$$O ={o_1,o_2,...o_T}$$的联合概率分布$$P(O,I|\lambda)$$，这样我们就可以很容易的求出边缘分布$$P(O|\lambda)$$了。

具体暴力求解的方法是这样的：首先，任意一个隐藏序列$$I = {i_1,i_2,...,i_T}$$出现的概率是：$$P(I|\lambda) = \pi_{i_1} a_{i_1i_2} a_{i_2i_3}... a_{i_{T-1};;i_T}$$

对于固定的状态序列$$I = {i_1,i_2,...,i_T}$$，我们要求的观察序列$$O ={o_1,o_2,...o_T}$$出现的概率是：$$P(O|I, \lambda) = b_{i_1}(o_1)b_{i_2}(o_2)...b_{i_T}(o_T)$$

则O和I联合出现的概率是：$$P(O,I|\lambda) = P(I|\lambda)P(O|I, \lambda) = \pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)...a_{i_{T-1};;i_T}b_{i_T}(o_T)$$

然后求边缘概率分布，即可得到观测序列O在模型$$\lambda$$下出现的条件概率$$P(O|\lambda)$$：$$P(O|\lambda) = \sum\limits_{I}P(O,I|\lambda) = \sum\limits_{i_1,i_2,...i_T}\pi_{i_1}b_{i_1}(o_1)a_{i_1i_2}b_{i_2}(o_2)...a_{i_{T-1};;i_T}b_{i_T}(o_T)$$

虽然上述方法有效，但是如果我们的隐藏状态数N非常多的那就麻烦了，此时我们预测状态有$$NT$$种组合，算法的时间复杂度是$$O(TNT)$$阶的。因此对于一些隐藏状态数极少的模型，我们可以用暴力求解法来得到观测序列出现的概率，但是如果隐藏状态多，则上述算法太耗时，我们需要寻找其他简洁的算法。

前向后向算法就是来帮助我们在较低的时间复杂度情况下求解这个问题的。

2. 用前向算法求HMM观测序列的概率

前向后向算法是前向算法和后向算法的统称，这两个算法都可以用来求HMM观测序列的概率。我们先来看看前向算法是如何求解这个问题的。

前向算法本质上属于动态规划的算法，也就是我们要通过找到局部状态递推的公式，这样一步步的从子问题的最优解拓展到整个问题的最优解。

在前向算法中，通过定义“前向概率”来定义动态规划的这个局部状态。什么是前向概率呢, 其实定义很简单：定义时刻t时隐藏状态为$$q_i$$, 观测状态的序列为$$o_1,o_2,...o_t$$的概率为前向概率。记为：$$\alpha_t(i) = P(o_1,o_2,...o_t, i_t =q_i | \lambda)$$

既然是动态规划，我们就要递推了，现在我们假设我们已经找到了在时刻t时各个隐藏状态的前向概率，现在我们需要递推出时刻t+1时各个隐藏状态的前向概率。

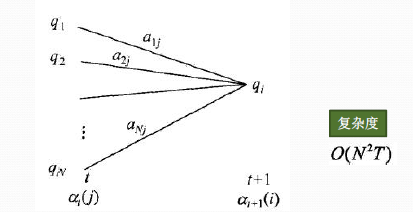
从下图可以看出，我们可以基于时刻t时各个隐藏状态的前向概率，再乘以对应的状态转移概率，即$$\alpha_t(j)a_{ji}$$就是在时刻t观测到$$o_1,o_2,...o_t$$，并且时刻t隐藏状态$$q_j$$, 时刻t+1隐藏状态$$q_i$$的概率。如果将想下面所有的线对应的概率求和，即$$\sum\limits_{j=1}^N\alpha_t(j)a_{ji}$$就是在时刻t观测到$$o_1,o_2,...o_t$$，并且时刻t+1隐藏状态$$q_i$$的概率。继续一步，由于观测状态$$o_{t+1}$$只依赖于t+1时刻隐藏状态$$q_i$$, 这样$$[\sum\limits_{j=1}^N\alpha_t(j)a_{ji}]b_i(o_{t+1})$$就是在在时刻t+1观测到$$o_1,o_2,...o_t, o_{t+1}$$，并且时刻t+1隐藏状态$$q_i$$的概率。而这个概率，恰恰就是时刻t+1对应的隐藏状态i的前向概率，这样我们得到了前向概率的递推关系式如下：$$\alpha_{t+1}(i) = \Big[\sum\limits_{j=1}^N\alpha_t(j)a_{ji}\Big]b_i(o_{t+1})$$

我们的动态规划从时刻1开始，到时刻T结束，由于$$\alpha_T(i)$$表示在时刻T观测序列为$$o_1,o_2,...o_T$$，并且时刻T隐藏状态$$q_i$$的概率，我们只要将所有隐藏状态对应的概率相加，即$$\sum\limits_{i=1}^N\alpha_T(i)$$就得到了在时刻T观测序列为$$o_1,o_2,...o_T$$的概率。

下面总结下前向算法。

输入：HMM模型$$\lambda = (A, B, \Pi)$$，观测序列$$O=(o_1,o_2,...o_T)$$

输出：观测序列概率$$P(O|\lambda)$$

1) 计算时刻1的各个隐藏状态前向概率：$$\alpha_1(i) = \pi_ib_i(o_1),; i=1,2,...N$$

2) 递推时刻2,3,...T时刻的前向概率：$$\alpha_{t+1}(i) = \Big[\sum\limits_{j=1}^N\alpha_t(j)a_{ji}\Big]b_i(o_{t+1}),; i=1,2,...N$$

3) 计算最终结果：$$P(O|\lambda) = \sum\limits_{i=1}^N\alpha_T(i)$$

从递推公式可以看出，我们的算法时间复杂度是$$O(TN2)$$，比暴力解法的时间复杂度$$O(TNT)$$少了几个数量级。

3. HMM前向算法求解实例

这里我们用隐马尔科夫模型HMM（一）HMM模型中盒子与球的例子来显示前向概率的计算。

我们的观察集合是:V={红，白}，M=2

我们的状态集合是：Q ={盒子1，盒子2，盒子3}， N=3

而观察序列和状态序列的长度为3.

初始状态分布为：$$\Pi = (0.2,0.4,0.4)^T$$

状态转移概率分布矩阵为：

$$A = \left( \begin{array} {ccc} 0.5 & 0.2 & 0.3 \ 0.3 & 0.5 & 0.2 \ 0.2 & 0.3 &0.5 \end{array} \right)$$

观测状态概率矩阵为：

$$B = \left( \begin{array} {ccc} 0.5 & 0.5 \ 0.4 & 0.6 \ 0.7 & 0.3 \end{array} \right)$$

球的颜色的观测序列:O={红，白，红}

按照我们上一节的前向算法。首先计算时刻1三个状态的前向概率：

时刻1是红色球，隐藏状态是盒子1的概率为：$$\alpha_1(1) = \pi_1b_1(o_1) = 0.2 \times 0.5 = 0.1$$

隐藏状态是盒子2的概率为：$$\alpha_1(2) = \pi_2b_2(o_1) = 0.4 \times 0.4 = 0.16$$

隐藏状态是盒子3的概率为：$$\alpha_1(3) = \pi_3b_3(o_1) = 0.4 \times 0.7 = 0.28$$

现在我们可以开始递推了，首先递推时刻2三个状态的前向概率：

时刻2是白色球，隐藏状态是盒子1的概率为：$$\alpha_2(1) = \Big[\sum\limits_{i=1}^3\alpha_1(i)a_{i1}\Big]b_1(o_2) = [0.10.5+0.160.3+0.28*0.2 ] \times 0.5 = 0.077$$

隐藏状态是盒子2的概率为：$$\alpha_2(2) = \Big[\sum\limits_{i=1}^3\alpha_1(i)a_{i2}\Big]b_2(o_2) = [0.10.2+0.160.5+0.28*0.3 ] \times 0.6 = 0.1104$$

隐藏状态是盒子3的概率为：$$\alpha_2(3) = \Big[\sum\limits_{i=1}^3\alpha_1(i)a_{i3}\Big]b_3(o_2) = [0.10.3+0.160.2+0.28*0.5 ] \times 0.3 = 0.0606$$

继续递推，现在我们递推时刻3三个状态的前向概率：

时刻3是红色球，隐藏状态是盒子1的概率为：$$\alpha_3(1) = \Big[\sum\limits_{i=1}^3\alpha_2(i)a_{i1}\Big]b_1(o_3) = [0.0770.5+0.11040.3+0.0606*0.2 ] \times 0.5 = 0.04187$$

隐藏状态是盒子2的概率为：$$\alpha_3(2) = \Big[\sum\limits_{i=1}^3\alpha_2(i)a_{i2}\Big]b_2(o_3) = [0.0770.2+0.11040.5+0.0606*0.3 ] \times 0.4 = 0.03551$$

隐藏状态是盒子3的概率为：$$\alpha_3(3) = \Big[\sum\limits_{i=1}^3\alpha_3(i)a_{i3}\Big]b_3(o_3) = [0.0770.3+0.11040.2+0.0606*0.5 ] \times 0.7 = 0.05284$$

最终我们求出观测序列:O={红，白，红}的概率为：$$P(O|\lambda) = \sum\limits_{i=1}^3\alpha_3(i) = 0.13022$$

4. 用后向算法求HMM观测序列的概率

熟悉了用前向算法求HMM观测序列的概率，现在我们再来看看怎么用后向算法求HMM观测序列的概率。

后向算法和前向算法非常类似，都是用的动态规划，唯一的区别是选择的局部状态不同，后向算法用的是“后向概率”，那么后向概率是如何定义的呢？

定义时刻t时隐藏状态为$$q_i$$, 从时刻t+1到最后时刻T的观测状态的序列为$$o_{t+1},o_{t+2},...o_T$$的概率为后向概率。记为：$$\beta_t(i) = P(o_{t+1},o_{t+2},...o_T, i_t =q_i | \lambda)$$

后向概率的动态规划递推公式和前向概率是相反的。现在我们假设我们已经找到了在时刻t+1时各个隐藏状态的后向概率$$\beta_{t+1}(j)$$，现在我们需要递推出时刻t时各个隐藏状态的后向概率。如下图，我们可以计算出观测状态的序列为$$o_{t+2},o_{t+3},...o_T$$， t时隐藏状态为$$q_i$$, 时刻t+1隐藏状态为$$q_j$$的概率为$$a_{ij}\beta_{t+1}(j)$$, 接着可以得到观测状态的序列为$$o_{t+1},o_{t+2},...o_T$$， t时隐藏状态为$$q_i$$, 时刻t+1隐藏状态为$$q_j$$的概率为$$a_{ij}b_j(o_{t+1})\beta_{t+1}(j)$$, 则把下面所有线对应的概率加起来，我们可以得到观测状态的序列为$$o_{t+1},o_{t+2},...o_T$$， t时隐藏状态为$$q_i$$的概率为$$\sum\limits_{j=1}^{N}a_{ij}b_j(o_{t+1})\beta_{t+1}(j)$$，这个概率即为时刻t的后向概率。

这样我们得到了后向概率的递推关系式如下：$$\beta_{t}(i) = \sum\limits_{j=1}^{N}a_{ij}b_j(o_{t+1})\beta_{t+1}(j)$$

现在我们总结下后向算法的流程,注意下和前向算法的相同点和不同点：

输入：HMM模型$$\lambda = (A, B, \Pi)$$，观测序列$$O=(o_1,o_2,...o_T)$$

输出：观测序列概率$$P(O|\lambda)$$

1) 初始化时刻T的各个隐藏状态后向概率：$$\beta_T(i) = 1,; i=1,2,...N$$

2) 递推时刻T-1,T-2,...1时刻的后向概率：$$\beta_{t}(i) = \sum\limits_{j=1}^{N}a_{ij}b_j(o_{t+1})\beta_{t+1}(j),; i=1,2,...N$$

3) 计算最终结果：$$P(O|\lambda) = \sum\limits_{i=1}^N\pi_ib_i(o_1)\beta_1(i)$$

此时我们的算法时间复杂度仍然是$$O(TN^2)$$。

5. HMM常用概率的计算

利用前向概率和后向概率，我们可以计算出HMM中单个状态和两个状态的概率公式。

1）给定模型$$\lambda$$和观测序列O,在时刻t处于状态$$q_i$$的概率记为:$$\gamma_t(i) = P(i_t = q_i | O,\lambda) = \frac{P(i_t = q_i ,O|\lambda)}{P(O|\lambda)}$$

利用前向概率和后向概率的定义可知：$$P(i_t = q_i ,O|\lambda) = \alpha_t(i)\beta_t(i)$$

于是我们得到：$$\gamma_t(i) = \frac{ \alpha_t(i)\beta_t(i)}{\sum\limits_{j=1}^N \alpha_t(j)\beta_t(j)}$$

2）给定模型$$\lambda$$和观测序列O,在时刻t处于状态$$q_i$$，且时刻t+1处于状态$$q_j$$的概率记为:$$\xi_t(i,j) = P(i_t = q_i, i_{t+1}=q_j | O,\lambda) = \frac{ P(i_t = q_i, i_{t+1}=q_j , O|\lambda)}{P(O|\lambda)}$$

而$$P(i_t = q_i, i_{t+1}=q_j , O|\lambda)$$可以由前向后向概率来表示为:$$P(i_t = q_i, i_{t+1}=q_j , O|\lambda) = \alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)$$

从而最终我们得到$$\xi_t(i,j)$$的表达式如下：$$\xi_t(i,j) = \frac{\alpha_t(i)a_{ij}b_j(o_{t+1})\beta_{t+1}(j)}{\sum\limits_{r=1}N\sum\limits_{s=1}N\alpha_t(r)a_{rs}b_s(o_{t+1})\beta_{t+1}(s)}$$

3) 将$$\gamma_t(i)$$和$$\xi_t(i,j)$$在各个时刻t求和，可以得到：

在观测序列O下状态i出现的期望值$$\sum\limits_{t=1}^T\gamma_t(i)$$

在观测序列O下由状态i转移的期望值$$\sum\limits_{t=1}^{T-1}\gamma_t(i)$$

在观测序列O下由状态i转移到状态j的期望值$$\sum\limits_{t=1}^{T-1}\xi_t(i,j)$$