# 二叉树

每个结点的度 均不超过 2 的 有序 树，称为 二叉树（binary tree）

1. 二叉树中每个结点的孩子数只能是 0、1 或 2 个，并且 每个孩子都有左右之分。
2. 位于左边的孩子称为左孩子，位于右边的孩子称为右孩子；
3. 以左孩子为根的子树称为左子树，以右孩子为根的子树称 为右子树

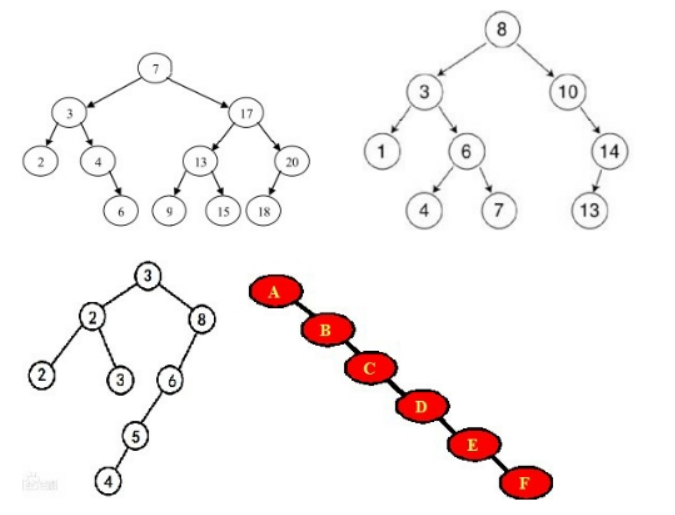
二叉查找/ 搜索/ 排序树 BST (binary search/sort tree) 或者是一棵空树； 或者是具有下列性质的二叉树： （1）若它的左子树不空，则左子树上所有结点的值均小于 它的根节点的值； （2）若它的右子树上所有结点的值均大于它的根节点的值； （3）它的左、右子树也分别为二叉排序树。

平衡二叉树 （Self-balancing binary search tree ） 自 平衡二叉查找树 又被称为 AVL 树（ 有别于 AVL 算法） 它是一 棵空树 或它的左右两个子树的高度差( 平衡因子 )的绝对值不超过 1 平衡二叉树： 每个结点的平衡因子都为 1、－1、0 的二 叉排序树。或者说每个结点的左右子树的高度最多差 1 的二 叉排序树。 平衡二叉树的目的是为了减少二叉查找树层次，提高查找速 度

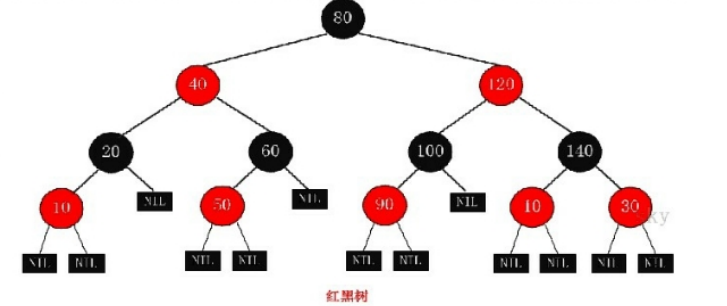
红黑树 R-B Tree，全称是 Red-Black Tree，又称为"红黑树"，它 一种平衡二叉树。红黑树的每个节点上都有存储位表示节点 的颜色，可以是红(Red)或黑(Black)。 红黑树的特性: （1）每个节点或者是黑色，或者是红色。 （2）根节点是黑色。 （3）每个叶子节点（NIL）是黑色。 [注意：这里叶子节点， 是指为空(NIL 或 NULL)的叶子节点！] （4）如果一个节点是红色的，则它的子节点必须是黑色的。 （5）从一个节点到该节点的子孙节点的所有路径上包含相 同数目的黑节点。 注意： (01) 特性(3)中的叶子节点，是只为空(NIL 或 null)的节点。 (02) 特性(5)，确保没有一条路径会比其他路径长出俩倍。因 而，红黑树是相对是接近平衡的二叉树

相比数组和链表，二叉树是一种比较独特的数据结构，树是一种非线性的数据结构，相对于线性的数据结构(链表、数组)而言，树的平均运行时间更短(往往与树相关的排序时间复杂度都不会高) 我们先来研究简单又经常用的---> 二叉树 1

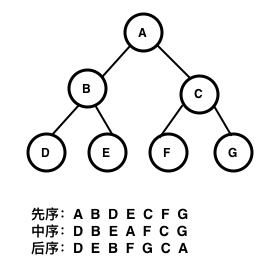
二叉树是由根节点N，左孩子节点L，右孩子节点R组成，那么这三个节点一共有 6 种排序方式，而实际上只有 3 种，另外 3 种只是顺序倒过来而已。这三种排序方式是： NLR、LNR、LRN，分别对应 先根、中根、后根遍历，先根即 N 在最前，中跟即 N 在中间，后根即 N 在最后。

首先创建二叉树节点

/**
 * 二叉树节点
 * @param <T>
 */
public class TreeNode<T> {
    //节点的属性-角标、数据、左节点、右节点
    private int index;
    private T data;
    private TreeNode leftChild;
    private TreeNode rightChild;
    //初始化节点
    public TreeNode(int index, T data) {
        this.index = index;
        this.data = data;
        this.leftChild = null;
        this.rightChild = null;
    }

    //getter，setter
    public int getIndex() {
        return index;
    }

    public void setIndex(int index) {
        this.index = index;
    }

    public T getData() {
        return data;
    }

    public void setData(T data) {
        this.data = data;
    }

    public TreeNode getLeftChild() {
        return leftChild;
    }

    public void setLeftChild(TreeNode leftChild) {
        this.leftChild = leftChild;
    }

    public TreeNode getRightChild() {
        return rightChild;
    }

    public void setRightChild(TreeNode rightChild) {
        this.rightChild = rightChild;
    }
}

创建二叉树

/**
 * 创建二叉树
 * @author yk
 */
public class BinaryTree {
    public TreeNode root = null;
    //用构造函数初始化根节点
    public BinaryTree() {
        root = new TreeNode<>(1, "A");
    }
    public void createBinaryTree() {
        TreeNode nodeB = new TreeNode<>(1, "B");
        TreeNode nodeC = new TreeNode<>(1, "C");
        TreeNode nodeD = new TreeNode<>(1, "D");
        TreeNode nodeE = new TreeNode<>(1, "E");
        TreeNode nodeF = new TreeNode<>(1, "F");
        TreeNode nodeG = new TreeNode<>(1, "G");
        root.setLeftChild(nodeB);
        root.setRightChild(nodeC);
        nodeB.setLeftChild(nodeD);
        nodeB.setRightChild(nodeE);
        nodeC.setLeftChild(nodeF);
        nodeC.setRightChild(nodeG);
    }
    //获取二叉树的高度
    public int getHeight() {
        return getHeight(root);
    }
    public int getHeight(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int leftHeight = getHeight(node.getLeftChild());
        int rightHeight = getHeight(node.getRightChild());
        return leftHeight > rightHeight ? (leftHeight + 1) : (rightHeight + 1);
    }
    //获取二叉树的大小
    public int getSize() {
        return getSize(root);
    }
    public int getSize(TreeNode node) {
        if (node == null) {
            return 0;
        }
        int leftSize = getSize(node.getLeftChild());
        int rightSize = getSize(node.getRightChild());
        return leftSize + rightSize + 1;
    }
    //先序遍历
    public void beforeOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        System.out.print(node.getData() + " ");
        beforeOrder(node.getLeftChild());
        beforeOrder(node.getRightChild());
    }
    //中序遍历
    public void midOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        midOrder(node.getLeftChild());
        System.out.print(node.getData() + " ");
        midOrder(node.getRightChild());
    }
    //后序遍历
    public void afterOrder(TreeNode node) {
        if (node == null) {
            return;
        }
        afterOrder(node.getLeftChild());
        afterOrder(node.getRightChild());
        System.out.print(node.getData() + " ");
    }
}