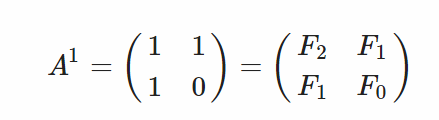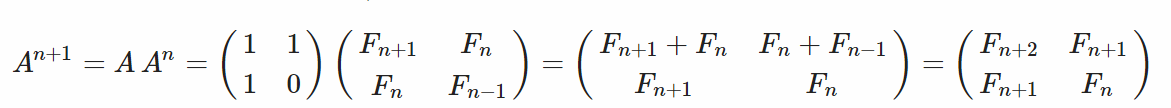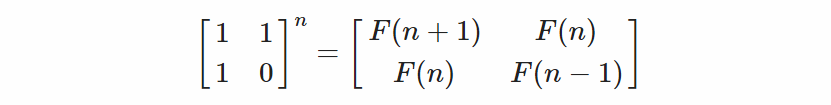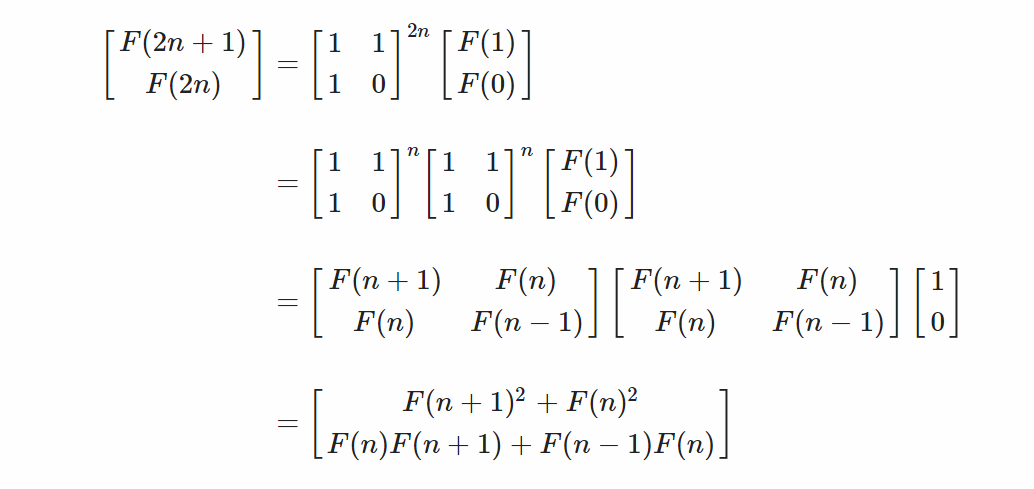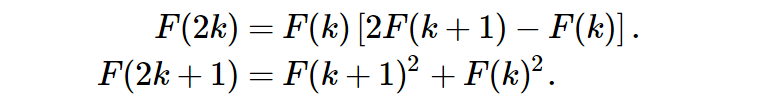遞迴呼叫篇
你所不知道的C語言:遞迴呼叫篇
「遞迴(recurse)只應天上有, 凡人該當用迴圈(iterate)」 Copyright (慣C) 2016 宅色夫 
- 請透過 gitter (線上對話服務,可透過 GitHub 或 Twitter 帳號登入) 提交疑問和建議事項: guts-general (按下去就對了) :::
案例分析:數列輸出
- 以下 C 程式的作用為何?
int p(int i, int N)
{
return (i < N && printf("%d\n", i) && !p(i + 1, N)) \
|| printf("%d\n", i);
}
- 拆解為以下兩部份:
- Line #3
(i < N && printf("%d\n", i) && !p(i + 1, N))- 依據 C Operator Precedence,
&&(Logical AND) operator 的運算規則為左值優先,只要左值不成立,右值都不會執行 - 因此我們可確定,當
i不小於N時,不會印出i,也不會呼叫p - printf(3) 會回傳印出的字元數目,這裡一定回傳非零值
- 接著我們可推斷,當
i < N成立,i會被輸出,接著會呼叫p - 換言之,中止條件是
i < N:::info 查詢 man page,對應到 GNU/Linux 的指令為man 3 printf:::
- 依據 C Operator Precedence,
- Line #4
|| printf("%d\n", i)||(Logical OR) operator 的運算規則為當左值成立時,右值就不會執行- 因此
p前面的!很重要。因為 p 的回傳值一定是 true (由於printf一定回傳非零值),而為確保會執行到這第二個printf,要將回傳值作 NOT,讓第一部份的結果為 false- 如果去掉 NOT,則只會輸出
i -> N:::info 把!p(i+1, N)的反相!拿掉後,得到以下結果:
/* i = 1 , n = 5 */ 1 2 3 4 5:::
- 如果去掉 NOT,則只會輸出
- 第二個
printf要等p執行完畢才會被執行。遞迴呼叫在實做層面來說,就是藉由 stack 操作,這裡一旦被 push 到 stack 印一次,被 pop 出來再印一次
綜合以上分析,我們可得知上述程式碼的作用為「印出 i -> N -> i 的整數序列,N 只會出現一次」。
-
延伸問題: 把
&&前後的敘述對調,是否影響輸出?- 也就是說,變更原始程式碼,從
i < N && printf("%d\n", i)改為printf("%d\n", i) && (i < N)的話 - 如果對調
printf跟i < N則會輸出i -> N N -> i(N 出現兩次) - 因為
printf會先被執行,不會受到i < N成立與否影響。
- 也就是說,變更原始程式碼,從
-
延伸問題:
i和N組合的有效上下界為何?- 科技公司的面試過程中,這類題目有助於測驗應試者的系統概念
- 不妨將原本程式碼改寫為以下:
#include <limits.h> #include <stdio.h> int p(int i, int N) { return (i < N && printf("%d\n", i) && !p(i + 1, N)) \ || printf("%d\n", i); } int main() { return p(0, INT_MAX); }- 在 Linux x86_64 環境編譯並執行後,會得到類似以下輸出: (數字可能會有出入)
261918 261919 261920 程式記憶體區段錯誤- 這裡的 segmentation fault 意味著 stack overflow,遞迴呼叫時,每一層都有變數存放於 stack 中,每次呼叫也要保存回傳位址 (return address) :::info 可用
ulimit -s來改 stack size,預設是 8 MB,計算後可推得,每個 stack 大約佔用 32 bytes,N 的限制取決於 stack size 的數值。 延伸閱讀: 通過ulimit 改善系統效能 ::: - 複習 你所不知道的C語言:函式呼叫篇,我們知道為了滿足 x86_64 ABI / calling convention,回傳位址佔 8 bytes, (int)
i和 (int)N這兩個變數合計 8 bytes, 函式的區域變數 (給printf()用的 format string 的位置) 8 bytes, p 回傳值 int 佔 4bytes ,總共 32 bytes。計算過程:
8MB = 8,388,608 bytes 8,388,608 / 32 = 262,144 次- 綜合上述,推算出
0 < N - i < 262144
-
實驗 (檔名為
p.c)
$ gcc -o p p.c -g
$ gdb -q p
Reading symbols from p...done.
(gdb) break p
Breakpoint 1 at 0x6ae: file p.c, line 7.
(gdb) run
Starting program: /tmp/p
Breakpoint 1, p (i=0, N=2147483647) at p.c:7
7 || printf("%d\n", i);
(gdb) info frame
Stack level 0, frame at 0x7fffffffdf60:
rip = 0x5555555546ae in p (p.c:7); saved rip = 0x555555554721
called by frame at 0x7fffffffdf70
source language c.
Arglist at 0x7fffffffdf50, args: i=0, N=2147483647
Locals at 0x7fffffffdf50, Previous frame's sp is 0x7fffffffdf60
Saved registers:
rbp at 0x7fffffffdf50, rip at 0x7fffffffdf58
:::warning 現代編譯器的最佳化可能會造成非預期的改變,比方說在前述編譯參數追加 -O3,在 gcc-6.2 輸出的執行檔會得到以下輸出: 523637 523638 523639 程式記憶體區段錯誤 :::
遞迴程式設計
Fibonacci sequence
數列值:
在費氏數列上其解法可分為下列
此數列之討論程度非常之高,解法也非常多元。下段我們選出幾種經典實做。
遞迴法 (Recursive)
即是費氏數列定義,將此轉為程式碼
int fib(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
return fib(n - 1) + fib (n - 2);
}
非遞迴法 (Iterative)
透過非遞迴方法可縮減原先使用遞迴法Call function所造成之成本。以下先討論基本方法。
int fib (int n)
{
int pre = -1;
int result = 1;
int sum = 0;
for (int i = 0; i <= n; i++) {
sum = result + pre;
pre = result;
result = sum;
}
return result;
}
我們可降低變數的使用:
int fib(int n)
{
int pre = -1;
int i = n;
n = 1;
int sum = 0;
while (i > 0) {
i--;
sum = n + pre;
pre = n;
n = sum;
}
return n;
}
Tail recursion
此法可加速原先之遞迴,可減少一半的資料回傳,而概念上是運用從第一次 call function 後即開始計算值,不像之前的遞迴需 call function 至中止條件後才開始計算值,再依序傳回到最上層,因此可大幅降低時間,減少 stack 使用量。參考實做如下:
int fib(int n, int a, int b)
{
if (n == 0) return a;
return fib(n - 1 , b, a + b);
}
此外,我們用樹狀突來解釋 Recursive Method 以及 Tail Recursion 之差別,以下以 Fib(5) 為例。
Recursive Method
Tail Recursion
在兩張樹狀圖之顯示下,可明顯看出複雜度之不同,一則會發展出樹狀結構,而另一則是有如迴圈。
Q-Matrix
透過矩陣轉換之方法,我們把原本之遞迴式轉換到矩陣表示,並透過矩陣次方之Divide and Conquer Method 來做加速。
因此能大幅減少預算量,但此方法牽涉除法以及矩陣,在撰寫傳寫組合語言上有一定之難度 ( 除法可使用右移以及可利用最後一個 Bit 來判斷奇偶數 ),在此參考演算法筆記之矩陣型別宣告實作Fibonacci Sequence。
int[][] matrix_multiply(int[][] a,int [][] b)
{
int t[2][2] = { { 0 , 0 } , { 0 , 0 } };
for (int i = 0 ; i < 2 ; i ++ )
for (int j = 0 ; j < 2 ; j ++ )
for (int k = 0 ; k < 2 ; k ++)
t[i][j] += a[i][k] * b[k][j];
return t;
}
// 使用 Divide-and-Conquer 方法加速矩陣次方
int[][] matrix_pow ( int a[][] , int n )
{
if ( n == 1 ) return a;
if (n % 2 == 0) {
int t[2][2];
t = matrix_pow(a , n >> 1);
return matrix_multiply(t , t);
} else {
int t1[2][2], t2[2][2];
t1 = matrix_pow(a, n >> 1 );
t2 = matrix_pow(a, n >> 1 + 1 );
return matrix_multiply(t1 , t2);
}
}
我們可在 Q-Matrix 的基礎上,計算 Fibonacci Sequence。
int fib(int n)
{
if (n < = 0) return 0;
int A1[2][2] = { { 1 , 1 } , { 1 , 0 } };
int result[2][2];
result = matrix_pow(A1, n);
return result[0][1];
}
**Fast doubling **
此方法類似上述提及之Q-Matrix做法,基於矩陣之方法繼續推演而得,在效能上更勝Q-Matrix一籌,此概念是使用矩陣乘法相將兩個n次方矩陣相乘而得。
透過上述之數學推論,我們最後可得兩公式可供使用。
接著我們即可使用此公式來撰寫Fibonacci Sequence。
int fib(int n)
{
if (n == 0) return 0;
int t0 = 1; // F(n)
int t1 = 1; // F(n + 1)
int t3 = 1; // F(2n)
int t4; // F(2n+1)
int i = 1;
while (i < n) {
if ((i << 1) <= n) {
t4 = t1 * t1+ t0 * t0;
t3 = t0 * (2 * t1 - t0);
t0 = t3;
t1 = t4;
i = i << 1;
} else {
t0 = t3;
t3 = t4;
t4 = t0 + t4;
i++;
}
}
return t3;
}
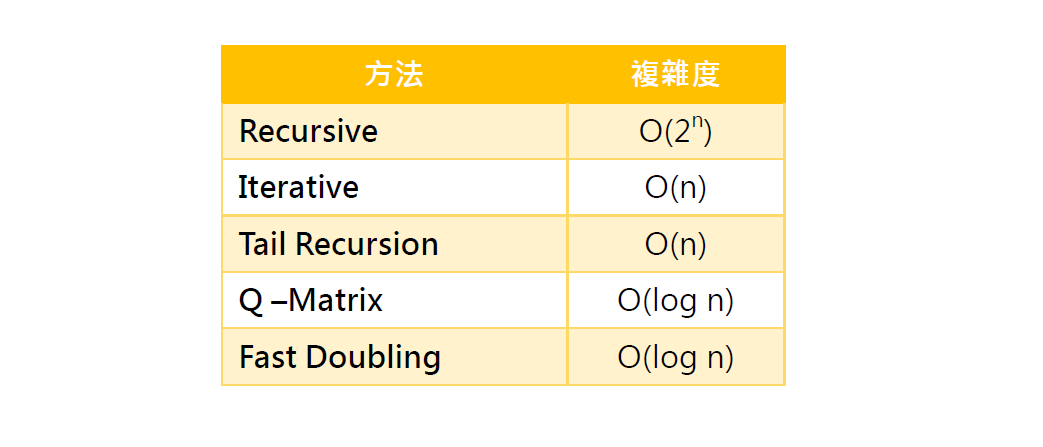
演算法比較
在以上之方法中,我們比較這些方法所花費之複雜度如下,可發現最基礎之Recursive 方法是極沒效率之方法,而其後之 Q-Matrix 及 Fast Doubling 效能則有顯著差異。
因改良後的時間複雜度皆為同等級,我們接著實際比較執行時間。
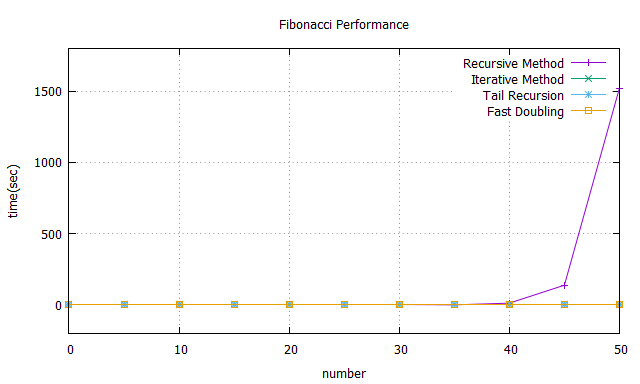
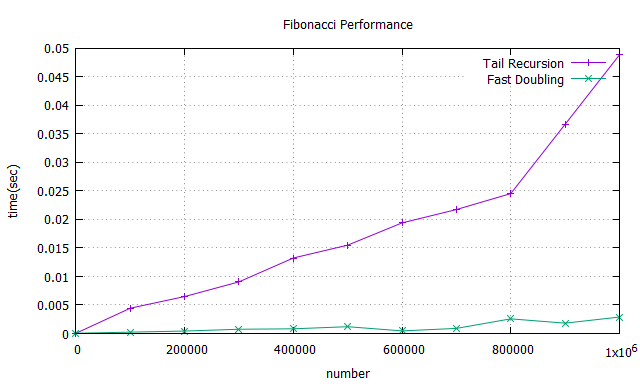
比較 Recursive Method 和 Iterative Method 的效能差異。
此兩種方法在 n = 1M 時還是都有不錯的表現,與原先之 Recusive method 相比實為甚廣,而透過此兩者之比較,最後還是可得出透過Fast Doubling 的方法能得到更好之效能,對上面之複雜度圖表也能互相呼應。
Fibonacci 參考資料
- Fibonacci number
- Tail call
- Fibonacci Q-Matrix
- How to prove Fibonacci sequence with matrices?
- 演算法筆記 - Q-Matrix
- Fast Fibonacci algorithms
- Need help understanding Fibonacci Fast Doubling Proof
案例分析:字串反轉
:::success ![]() 據說某些 M 開頭的科技公司面試很喜歡出這題 :::
據說某些 M 開頭的科技公司面試很喜歡出這題 :::
- 要求:用 C 語言實做
char *reverse(char *s),反轉 NULL 結尾的字串,限定 in-place 與遞迴 - 先思考實做 swap 的技巧,考慮以下程式碼:
void swap(int *a, int *b)
{
int t = *a; *a = *b; *b = t;
}
能否避免使用區域變數 t?又,可否改用 bit-wise operator 來改寫?
-
數值運算:利用兩個相差距離做運算,但若遇到一個很大的整數與一個負數(足夠讓他超過最大整數)兩個相減時,會產生益位
*a = *a - *b; //兩數相差 *b = *a + *b; //相加得出*b *a = *b - *a; //相減得出*a -
邏輯運算:運用邏輯運算查看出兩個不同相差的位元,依據以下真值表:
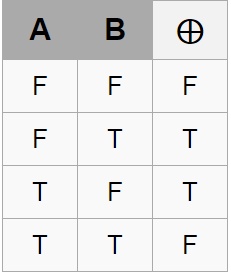
*a = *a ^ *b; // 求得相差位元 *b = *a ^ *b; // 與相差位元做 XOR 得出 *a *a = *a ^ *b; // 與相差位元做 XOR 得出 *b
邏輯運算的好處是,可避免前述算術會遇到的 integer overflow,而且不限定位元數
- 參考的 in-place string reverse 想法:一直 swap '\0'之前的character: :::info a b c ==d== ==e== -> a b c ==e== ==d== a b ==c== ==e== d -> a b ==e== ==c== d a b e ==c== ==d== -> a b e ==d== ==c== a ==b== ==e== d c -> a ==e== ==b== d c a e b ==d== ==c== -> a e b ==c== ==d== a e ==b== ==c== d -> a e ==c== ==b== d a e c ==b== ==d== -> a e c ==d== ==b== ==a== ==e== c d b -> ==e== ==a== c d b e a ==c== ==d== b -> e a ==d== ==c== b e a d ==c== ==b== -> e a d ==b== ==c== e ==a== ==d== b c -> e ==d== ==a== b c e d a ==b== ==c== -> e d a ==c== ==b== e d ==a== ==c== b -> e d ==c== ==a== b e d c ==a== ==b== -> e d c ==b== ==a== :::
static inline void swap(char *a, char *b)
{
*a = *a ^ *b; *b = *a ^ *b; *a = *a ^ *b;
}
char *reverse(char *s)
{
if ((*s == '\0') || if (*(s + 1) == '\0'))
return NULL;
reverse(s + 1);
swap(s, (s + 1));
if (reverse(s+2) != '\0')
reverse(s+2);
reverse(s+1);
}
案例分析: 類似 find 的程式
- 給定 opendir(3) 與 readdir(3) 函式,用遞迴寫出類似 find 的程式
- find 的功能:列出包含目前目錄和其所有子目錄之下的檔案名稱
#include <sys/types.h>
#include <dirent.h>
void list_dir(const char *dir_name)
{
DIR *d = opendir(dir_name);
// fail to open directory
if (!d) return;
while (1) {
struct dirent *entry = readdir(d);
if (!entry) break;
const char *d_name = entry->d_name;
printf ("%s/%s\n", dir_name, d_name);
if ((entry->d_type & DT_DIR)
&& !strcmp(d_name, "..") && !strcmp(d_name, ".")) {
char path[PATH_MAX];
int path_length = snprintf(path, PATH_MAX,
"%s/%s", dir_name, d_name);
printf ("%s\n", path);
// path is too long
if (path_length >= PATH_MAX) return;
/* Recursively call "list_dir" with new path. */
list_dir (path);
}
}
if (closedir (d)) return;
}
- 練習: 如何連同檔案一併列印?
- 練習:上述程式碼實做有誤,額外的
.和..也輸出了,請修正 source: rd.c
案例分析: Merge Sort
- Program for Merge Sort in C: 內含動畫
- Merge Sort: 複雜度分析
- 進行中: MapReduce with POSIX Thread
案例分析: Bubble Sort
- Bubble Sort: non-recursive vs. recursive
函數式程式開發
- Functional programming 在 concurrency 環境 變得日益重要
- Functional C
- Functional programming in C
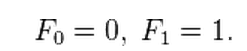


.png)