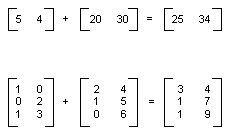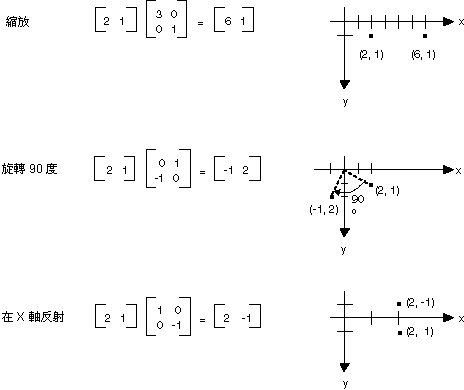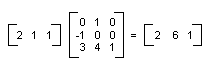以矩陣來表示轉換
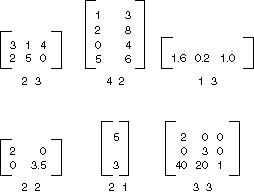
m×n 矩陣是按照 m 資料列和 n 資料行排列的一組數字。 下圖將顯示幾種矩陣。
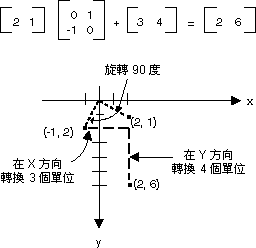
您可以利用增加個別項目來加入兩個大小相同的矩陣。 下圖將顯示兩個矩陣加法範例。
m×n 矩陣可乘以 n×p 矩陣,其產生的結果便為 m×p 矩陣。 第一個矩陣的資料行數目必須和第二個矩陣的資料列數目相同。 例如,4×2 矩陣可乘以 2×3 矩陣以產生 4×3 矩陣。 平面上的點和矩陣的資料列和資料行都可視為向量。 例如,(2, 5) 是具有兩個元件的向量,而 (3, 7, 1) 是具有三個元件的向量。 這兩種向量所產生的點的定義如下:
(a, b)•(c, d) = ac + bd
(a, b, c)‧(d, e, f) = ad + be + cf
例如,(2, 3) 和 (5, 4) 產生的點是 (2)(5) + (3)(4) = 22。 (2, 5, 1) 和 (4, 3, 1) 產生的點是 (2)(4) + (5)(3) + (1)(1) = 24。 請注意,這兩種向量所產生的點是數字,而非另一個向量。 此外,只有當這兩個向量擁有相同的元件數目時,您才可以計算產生的點數目。
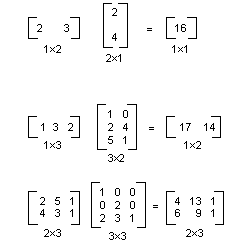
假設 A(i, j) 是矩陣 A 第 i 個資料列和第 j 個資料行中的項目。 例如 A(3, 2) 是矩陣 A 第 3 個資料列和第 2 個資料行中的項目。 假設 A、B 和 C 都是矩陣,而 AB = C。 C 項目的計算結果如下: C(i, j) = (A 的第 i 個資料列)‧(B 的第 j 個資料行) 下圖將顯示數個矩陣乘法的範例。
如果將平面中的點視為 1×2 矩陣,您可以將該矩陣乘以 2×2 矩陣以進行轉換。 下圖將說明數個套用到點 (2, 1) 的轉換。
上圖所顯示的所有變換皆為線性變換。其他特定變換是非線性的,例如轉換,而且無法乘以 2×2 矩陣來表示。假設您想要以點 (2, 1) 作為開始、將它旋轉 90 度、在 X 方向轉換 3 個單位和在 Y 方向轉換 4 個單位。您可以使用矩陣加法之後的矩陣乘法來完成這項作業。
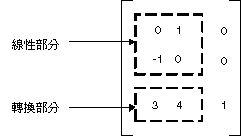
轉換 (加上 1×2 矩陣) 之後的線性變換 (乘以 2×2 矩陣) 稱為仿射變換。另一種將仿射變換儲存為矩陣組 (其中一個作為線性部分,另一個作為轉換部分) 的方法是將整個變換儲存在 3×3 矩陣中。要有效完成這項工作,平面的其中一點必須儲存為虛設 3rd 座標中的 1×3 矩陣。常用的技巧是將所有 3rd 座標變成 1,例如,點 (2, 1) 便以矩陣 [2 1 1] 來表示。下圖將顯示仿射變換 (旋轉 90 度;在 X 方向變換 3 個單位、在 Y 方向轉換 4 個單位) 將乘以 3×3 矩陣來表示。
上例中,點 (2, 1) 將對應到點 (2, 6)。請注意:3×3 矩陣的第三個資料行包含數字 0、0 和 1。仿射變換的 3×3 矩陣一律都是這樣。資料行 1 和 2 中的六個數字非常重要。矩陣的左上 2×2 部份代表變換的線性部分,而第三個資料列的前兩個項目則代表轉換。
在 GDI+ 中,您可以將仿射變換儲存在 Matrix 物件中。由於用來表示仿射變換的矩陣第三個資料行一律為 (0, 0, 1),因此在建立 Matrix 物件時,您只能指定前兩個資料行中的六個數字。陳述式 (Statement) Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) 將建立上圖所顯示的矩陣。
##複合變換
| 矩陣 A | 旋轉 90 度 |
| 矩陣 B | 在 X 方向縮放 2 個係數 |
| 矩陣 C | 在 Y 方向轉換 3 個單位 |
如果我們從點 (2, 1) 開始— 由矩陣 [2 1 1] 代表 — 並且乘以 A,然後乘以 B,然後再乘以 C,點 (2, 1) 將會在列出的順序中經歷三種變換。
[2 1 1]ABC = [-2 5 1]
如果您不想將複合變換的三個部分儲存在三個個別的矩陣中,您可以同時乘以 A、B 和 C 以取得儲存整個複合變換的單一 3×3 矩陣。假設 ABC = D。則任何一個點乘以 D 所得的結果都等於任何一個點乘以 A、然後 B、然後 C。
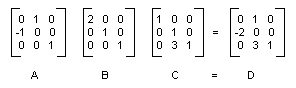
[2 1 1]D = [-2 5 1] 下圖將顯示矩陣 A、B、C 和 D。
複合變換是由變換序列組成,其中序列會緊跟著另一個序列。舉下表的矩陣和變換為例:
複合變換的矩陣的形成可藉由乘以單獨變換矩陣便可達成,這表示仿射變換的任何序列都可以儲存在單一 Matrix 物件中。 警告 複合變換的順序非常重要。通常,旋轉、然後縮放、然後轉換與縮放、然後旋轉、然後在轉換並不相同。同樣的,矩陣乘法的順序也很重要。一般而言,ABC 與 BAC 並不相同。 Matrix 類別提供了幾個方法,用來建置 (Build) 複合變換:Multiply、Rotate、RotateAt、Scale、Shear 和 Translate。下列範例建立複合變換矩陣,它會先旋轉 30 度、然後在 Y 方向縮放 2 個係數,然後在 X 方向轉換 5 個單位:
- VB
Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)
[C#]
Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);
下列圖示將顯示該矩陣。