編程判斷兩個鏈表是否相交
這是一道廣為流傳的題目: 編程判斷兩個鏈表是否相交;原題假設“不帶環”,所以只要想通了之後很簡單;但是,若要考慮帶環的情況,那麼要注意的點就很多了。 其實可以把無環和有環的情況全都包括在一個方法實現內解決。
分析
首先,無環的情況;無環是《編程之美》原書裡的題目,很多人都反應說這個題相對書中其它題來講太過於簡單了。也確實,只要在紙上把“所有單向鏈表相交的情況”畫出來很容易就能想通解法了(只要正確理解題意,那麼“兩個無環單向鏈表”畫出來只可能是2條不相干的鏈表或一個”Y”字形) —— 所以,判斷兩個不帶環的鏈表是否相交,只要將兩個鏈表的頭指針都移到鏈表尾,然後比較尾指針地址是否相等就可以了。 如果帶環,個人總結,要明白以下幾點:
- 無環鏈表和有環鏈表是不可能相交的個
- 有環鏈表若相交,其“整個環上”的所有node一定都鏈
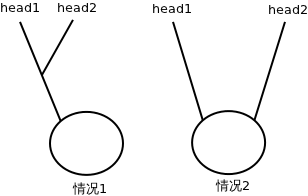
- 表的相交,情況只有2種:相交於”環上”或相交於”不是環的部分”,即下圖所示;兩種情況都需要使用“兩個指針的追逐”方法來判斷兩個鏈表的環部分是否相交;
- 有關鏈表追逐的考慮: 相對速度、距離、時間要算好,否則很容易漏掉幾種邊界情況;
#include <stdio.h>
// define the node struct of links
typedef struct Node {
struct Node* next;
} Node;
int is_intersected(Node* p1, Node* p2);
Node* has_circle(Node* head);
int main(int args, char** argv)
{
Node end1 = { NULL };
Node end2 = { NULL };
// 定義幾種鏈表情況
// two links not intersect with each other, no circle
Node link_1_n = {
&(Node)
{
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&end1
}
}
}
}
}
}
}
}
};
Node link_2_n = {
&(Node)
{
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&end2
}
}
}
}
}
}
}
}
};
// two links intersect with each other, no circle
Node common_n = { &(Node)
{
&(Node) {
&end1
}
}
};
Node link_1_y = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&common_n
}
}
}
}
}
};
Node link_2_y = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&(Node) {
&common_n
}
}
}
}
}
};
// two links, has circle, not intersected.
Node circle1 = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&circle1
}
}
}
}
};
Node link_c1_n = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&circle1
}
}
}
}
};
Node circle2 = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&circle2
}
}
}
}
};
Node link_c2_n = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&circle2
}
}
}
}
};
// two links, has circle, intersected at a non-circle position
Node common_c = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&common_c
}
}
}
}
};
Node common_part = { &(Node)
{
&common_c
}
};
Node link_c1_y = { &(Node)
{
&(Node) {
&common_part
}
}
};
Node link_c2_y = { &(Node)
{
&(Node) {
&common_part
}
}
};
// two links, has common circle, but different 'joint-points'.
Node jp1 = { NULL };
Node jp2 = { NULL };
// 'weave' the joint-points into a circle:
jp1.next = &(Node) {
&(Node) {
&jp2
}
};
jp2.next = &(Node) {
&jp1
};
Node link_c1_y2 = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&jp1
}
}
}
}
};
Node link_c2_y2 = { &(Node)
{
&(Node) {
&(Node) {
&(Node) {
&jp2
}
}
}
}
};
if (is_intersected(&link_1_n, &link_2_n)) {
printf("link_1_n and link_2_n Intersected!\n");
}
if (is_intersected(&link_1_y, &link_2_y)) {
printf("link_1_y and link_2_y Intersected!\n");
}
if (is_intersected(&link_c1_n, &link_c2_n)) {
printf("link_c1_n and link_c2_n Intersected!\n");
}
if (is_intersected(&link_c1_y, &link_c2_y)) {
printf("link_c1_y and link_c2_y Intersected!\n");
}
if (is_intersected(&link_c1_y2, &link_c2_y2)) {
printf("link_c1_y2 and link_c2_y2 Intersected!\n");
}
return 0;
}
int is_intersected(Node* p1, Node* p2)
{
Node* has_circle_1 = has_circle(p1);
Node* has_circle_2 = has_circle(p2);
if (has_circle_1) {
if (has_circle_2) {
Node* pp1 = has_circle_1;
Node* pp2 = has_circle_2;
if (pp1 == pp2 || pp1->next == pp2) {
return 1;
}
while (pp1->next != has_circle_1) {
pp1 = pp1->next;
pp2 = pp2->next->next;
if (pp1 == pp2) {
return 1;
}
}
return 0;
} else {
return 0;
}
} else {
if (has_circle_2) {
return 0;
} else {
while (p1->next) {
p1 = p1->next;
}
while (p2->next) {
p2 = p2->next;
}
return p1 == p2;
}
}
return 0;
}
Node* has_circle(Node* head)
{
Node* p1;
Node* p2;
p1 = p2 = head;
if (p2->next != NULL) {
p2 = p2->next;
} else {
return NULL;
}
while (p2->next != NULL && p2->next->next != NULL) {
p1 = p1->next;
p2 = p2->next->next;
if (p1 == p2) {
return p1;
}
}
return NULL;
}
其中,has_circle方法是判斷一個單向鏈表是否帶環的,基本原理就是設置2個“速度”不同的鏈表,快的去追慢的,追上就是帶環,直到較快指針遇到null還沒追上就是沒有環;假設環包含n個節點,指針p2的”速度”是2,p1的速度是1,相對速度就是1,從相同一點出發的話,p2追上p1至少要n步;若再假設該鏈表除了環的部分外還帶有一個長度為k的“尾巴”,那麼追上的步數最多是n+k;也就是線性時間複雜度內就能完成這個判斷。
這提供了一種很好的判斷是否”環狀”的思路;以前我只寫過“用一個棧來記錄”的方式,弱爆了…(時間複雜度為O(n2))
在has_circle_1和has_circle_2都滿足的時候,也就是說2個鏈表都帶環的時候,要分別取2個環上的一點來玩“追逐遊戲”來判斷是否相交;在這段程序裡是pp1和pp2;然後一個速度為2一個速度為1開始玩“追逐遊戲”,當慢的那個走完環上所有節點時快的那個還沒追上它的話,說明不相交(此時耗費時間n——即環節點數;因為快慢指針的相對速度為1,快指針理應在時間n以內追上慢鏈表,否則不相交)。
##總結
單向鏈表的問題…著實不簡單,可以相當複雜…對於這種關乎“形狀”的問題,在紙上畫一畫會很有幫助。